Chapter 2
Exercises 2.1
-
1.
parametric equations
-
3.
displacement
-
5.
[-2]
-
7.
[-2]
-
9.
[-2]
-
11.
[-2]
-
13.
[-]
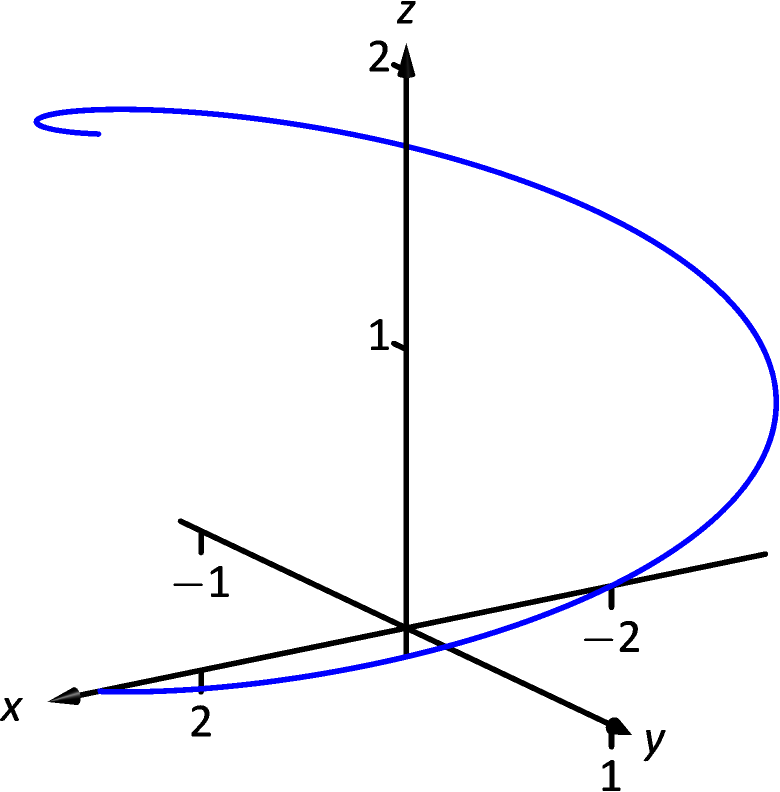
-
15.
[-]
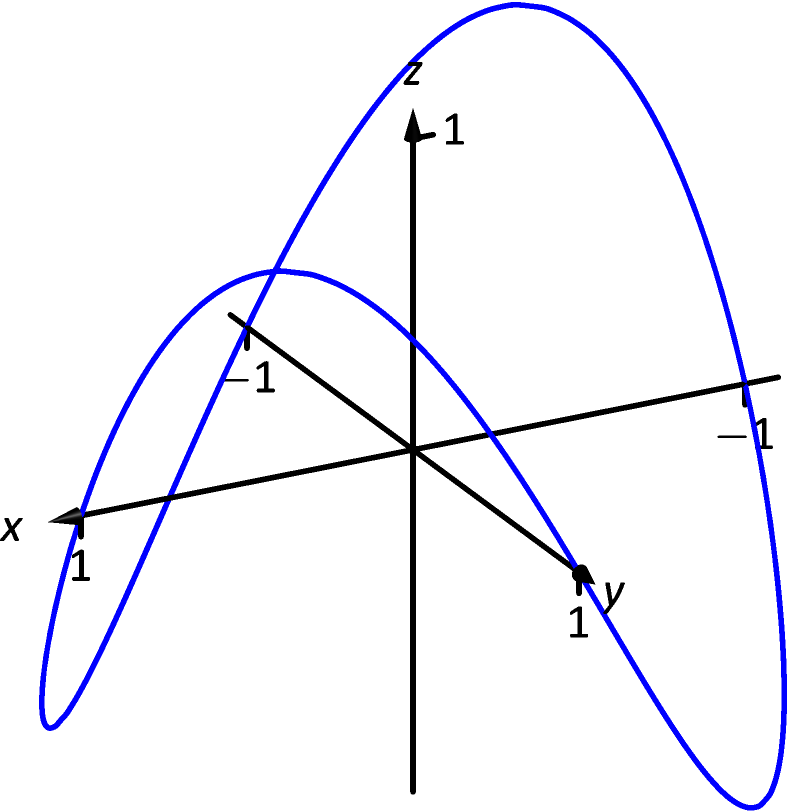
-
17.
.
-
19.
.
-
21.
Answers may vary; three solutions are
,
and
.
-
23.
Answers may vary, though most direct solutions are
,
and
.
-
25.
Answers may vary, though most direct solutions are
,
,
and
.
-
27.
Answers may vary, though most direct solution is
.
-
29.
Answers may vary, though most direct solution is .
-
31.
-
33.
Exercises 2.2
-
1.
component
-
3.
It is difficult to identify the points on the graphs of and that correspond to each other.
-
5.
-
7.
-
9.
-
11.
-
13.
-
15.
[-2]
-
17.
[-2]
-
19.
-
21.
-
23.
, where is an integer;
so
-
25.
is not smooth at , where is an integer
-
27.
Both derivatives return .
-
29.
Both derivatives return
.
-
31.
-
33.
-
35.
-
37.
-
39.
-
41.
-
43.
-
45.
Exercises 2.3
-
1.
Velocity is a vector, indicating an objects direction of travel and its rate of distance change (i.e., its speed). Speed is a scalar.
-
3.
The average velocity is found by dividing the displacement by the time traveled – it is a vector. The average speed is found by dividing the distance traveled by the time traveled – it is a scalar.
-
5.
One example is traveling at a constant speed in a circle, ending at the starting position. Since the displacement is , the average velocity is , hence . But traveling at constant speed means the average speed is also .
-
7.
,
-
9.
,
-
11.
,
-
13.
,
-
15.
.
Min at ; Max at .
-
17.
.
Speed is constant, so there is no difference between min/max
-
19.
.
min: ; max:
-
21.
.
speed is constant, so there is no difference between min/max
-
23.
.
min: ; max: there is no max; speed approaches as
-
25.
[-2]
-
(a)
;
-
(b)
; ;
; ;
-
(a)
-
27.
[-2]
-
(a)
;
-
(b)
; ;
; ;
-
(a)
-
29.
,
-
31.
,
-
33.
Displacement: ; distance traveled: ft; average velocity: ; average speed: ft/s
-
35.
Displacement: ; distance traveled: ft; average velocity: ; average speed: ft/s
-
37.
At -values of seconds, where is an integer.
-
39.
[-2]
-
(a)
Holding the crossbow at an angle of radians, will hit the target s later. (Another solution exists, with an angle of , landing s later, but this is impractical.)
-
(b)
In the .4 seconds the arrow travels, a deer, traveling at 20mph or 29.33ft/s, can travel 11.7ft. So she needs to lead the deer by 11.7ft.
-
(a)
-
41.
The position function is . The -component is 0 when ; , meaning the box will travel about 1740ft horizontally before it lands.
Exercises 2.4
-
1.
1
-
3.
and .
-
5.
;
-
7.
. (Be careful; this cannot be simplified as just as , but rather .)
-
9.
; in parametric form,
-
11.
; in parametric form,
-
13.
;
-
15.
;
-
17.
[-2]
-
(a)
Be sure to show work
-
(b)
-
(a)
-
19.
[-2]
-
(a)
Be sure to show work
-
(b)
-
(a)
-
21.
;
-
23.
;
-
25.
and
At , and ;
At , and .
At , all acceleration comes in the form of changing the direction of velocity and not the speed; at , more acceleration comes in changing the speed than in changing direction.
-
27.
and
At , and ;
At , and .
The object moves at constant speed, so all acceleration comes from changing direction, hence . is always parallel to , but twice as long, hence .
-
29.
and
At , and ;
At , and .
The object moves at constant speed, meaning that is always 0. The object “rises” along the -axis at a constant rate, so all acceleration comes in the form of changing direction circling the -axis. The greater the radius of this circle the greater the acceleration, hence .
Exercises 2.5
-
1.
time and/or distance
-
3.
Answers may include lines, circles, helixes
-
5.
-
7.
, so
-
9.
, so
-
11.
;
, .
-
13.
;
,
-
15.
;
,
-
17.
;
,
-
19.
;
,
-
21.
;
,
-
23.
maximized at
-
25.
maximized at
-
27.
radius of curvature is .
-
29.
radius of curvature is .
-
31.
, or
-
33.
, or
-
35.
Let and apply the second formula of part 3.
