1.0 Chapter Prerequisites

The material in this section provides a basic review of and practice problems for pre-calculus skills essential to your success in Calculus. You should take time to review this section and work the suggested problems (checking your answers against those in the back of the book). Since this content is a pre-requisite for Calculus, reviewing and mastering these skills are considered your responsibility. This means that minimal, and in some cases no, class time will be devoted to this section. When you identify areas that you need help with we strongly urge you to seek assistance outside of class from your instructor or other student tutoring service.

Functions

A function $f$ is a rule that assigns each element $x$ from a set (called the domain) to exactly one element, called $f(x)$ , in another set. Unless we say otherwise, the domain is the set of all real numbers for which the rule makes sense and defines a real number. All possible values of $f(x)$ are called the range of $f$ . We use four ways to represent a function.

•

By a graph
•

By an explicit formula
•

By a table of values
•

By a verbal description

Throughout the book we will use several representations of any given function to help give us a better understanding of the problem. The graphs in Figure 1.0.1 contain most of the base functions we can use to build other functions using transformations.

y=x^{2}

y=x^{3}

y=e^{x}

y=\sin x

y=\left\lvert x\right\rvert

y=\sqrt{x}

y=\sqrt[3]{x}

y=\ln x

y=\cos x

y=\dfrac{1}{x}

Figure 1.0.1: Basic Function Graphs

We will often transform these functions into other functions as given in the next two figures.
The function shifts $f(x)$ $y=f(x)+c$ $c$ units upward $y=f(x)-c$ $c$ units downward $y=f(x+c)$ $c$ units left $y=f(x-c)$ $c$ units right Figure 1.0.2: Translations of Basic Functions with $c>0$

The function transforms

f(x)

y=cf(x)

stretching vertically by a factor of

c

y=\frac{1}{c}f(x)

shrinking vertically by a factor of

c

y=f(cx)

shrinking horizontally by a factor of

c

y=f(\frac{x}{c})

stretching horizontally by a factor of

c

y=-f(x)

reflecting about the

x

-axis

y=f(-x)

reflecting about the

y

-axis Figure 1.0.3: Scaling Basic Functions with

c>1

Domain

We said above that domain is the set of real numbers for which the function (rule) defines a real number and makes sense. Ask yourself, “what values can I put into the function and get a real value out?” There are generally two key expressions that will limit the domain of a function from all real numbers. We may not divide by zero and we may not have a negative number underneath an even root. The following examples illustrate how we restrict the domain when we see these expressions.

Example 1.0.1 Finding a domain

Find the domain of the function $f(x)=\sqrt{x-4}$ .

SolutionThe square root of a negative number is not defined as a real number so the domain of $f$ will be all real numbers for which $x-4\geq 0$ which is $x\geq 4$ . In interval notation, this is $[4,\infty)$ .

Example 1.0.2 Finding a domain

Find the domain of the function $g(x)=\dfrac{3}{x^{2}-9}$ .

SolutionWe cannot divide by zero so we factor the denominator of $g$ and exclude those values where the denominator is zero.

g(x)=\frac{3}{x^{2}-9}=\frac{3}{(x-3)(x+3)}

We see that $x\neq 3,-3$ for $g$ to be defined, which is written in interval notation as $(-\infty,-3)\cup(-3,3)\cup(3,\infty)$ .

Example 1.0.3 Finding a domain

Find the domain of the function $h(x)=\dfrac{1}{\sqrt{x^{2}-4}}$

SolutionFor $h$ to be defined as a real number we must have $x^{2}-4>0$ . This is equivalent to $(x-2)(x+2)>0$ and we create a sign chart:

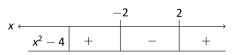
This shows that $x^{2}-4$ will be greater than zero on $(-\infty,-2)\cup(2,\infty)$ .

Exercises 1.0

Problems

In Exercises 1–10., find the domain of the given function.

1.

$g(x)=(x-3)^{2}+5$
2.

$f(x)=\sqrt{x+7}-3$
3.

$f(x)=\sqrt{x^{2}-6x-7}$
4.

$f(x)=3\left\lvert x-2\right\rvert+4$
5.

$f(x)=\dfrac{x-3}{x^{2}-4x+4}$
6.

$g(x)=\dfrac{x-3}{x^{2}-x+6}$
7.

$h(x)=\sin(x+3\pi)$
8.

$f(x)=\dfrac{4x+1}{\sqrt{x^{2}-4}}$
9.

$h(x)=\dfrac{\cos x}{x}$
10.

$g(x)=\left\lvert x^{2}-x-6\right\rvert$

In Exercises 11–14., graph the given $f$ .

11.

$f(x)=\begin{cases}x^{2}-3&x<2\\ x-4&x\geq 2\end{cases}$
12.

$f(x)=\begin{cases}3&x\leq-1\\ 2-x^{2}&-1<x<2\\ -3&x\geq 2\end{cases}$
13.

$f(x)=\begin{cases}x+3&x<-2\\ x^{2}+4&-2\leq x\leq 3\\ e^{-x}&x>3\end{cases}$
14.

$f(x)=\begin{cases}\sin x&x\leq 0\\ \frac{1}{2}x+1&x>0\end{cases}$

In Exercises 15–18., evaluate the expressions for the given $f$ .

15.
$f(x)=3x^{2}-2x+6$ (a) $f(2)$ (b) $f(-1)$ (c) $f(a)$ (d) $f(x+h)$ (e) $\dfrac{f(x+h)-f(x)}{h}$
16.
$f(x)=\sqrt{x-2}$ (a) $f(4)$ (b) $f(-3)$ (c) $f(t)$ (d) $f(x+h)$ (e) $\dfrac{f(x+h)-f(x)}{h}$
17.
$f(x)=\dfrac{1}{x}$ (a) $f(-1)$ (b) $f(9)$ (c) $f(t+3)$ (d) $f(x+h)$ (e) $\dfrac{f(x+h)-f(x)}{h}$
18.
$f(x)=e^{x}$ (a) $f(-2)$ (b) $f(3)$ (c) $f(t+1)$ (d) $f(x+h)$ (e) $\dfrac{f(x+h)-f(x)}{h}$

In Exercises 19–22., use sign diagrams to find the solutions to the nonlinear inequalities.

19.

$\dfrac{(x-2.13)(x-2.12)^{2}}{(2.15-x)(x-2.14)^{3}}\leq 0$
20.

$\dfrac{(5.678-x)^{3}(x-5.677)}{(x-5.679)^{2}}\leq 0$
21.

$\dfrac{1}{x-0.3}\geq 2$
22.

$\dfrac{x}{0.1-x}\leq-2$