UND MATHEMATICS TRACK MEET Individual Test 2

University of North Dakota Grades 11/12
January 12, 2026
School Team Name
Calculators are NOT allowed. Solutions Student Name

• 1.

  Let $f$ be a function satisfying

  $$f(f(n))+f(n)=2n+3,$$

  and $f(n)$ is a natural number for all natural numbers $n$. Find $f(2026)$.

  (a) $2025$    (b) $2026$    (c) $2027$    (d) $2028$    (e) $2029$

    (2 pts) 1. (c)

  Solution: Since $f$ is an increasing function, we must have $f(n)>n$ for all $n$. Indeed, suppose on the contrary that $f(n)\le n$ for some $n$, we have

  $$f(f(n))+f(n)\le f(n)+n\le n+n=2n>2n+3,$$

  which is a contradiction. Putting $g(n)=f(n)-n$, we must have $g(n)>0$ for all $n$, which deduces that

  $$f(f(n))=f(n)+g(f(n))=g(n)+n+g(n+g(n)).$$

  Combining this with the assumption, we have

  $$2n+3=f(f(n))+f(n)=2(g(n)+n)+g(n+g(n)).$$

  In other words,

  $$2g(n)+g(n+g(n))=3,$$

  which implies that for all $n$. Since $g(n)$ is a natural number, we must have $g(n)=1$ for all $n$. This means that $f(n)=n+1$ for all $n.$ So $f(2026)=2027.$

• 2.

  For how many integers $n\ge 0$ is $n^2+6n+5$ a perfect square?

  (a) $0$    (b) $1$    (c) $2$    (d) $3$    (e) infinitely many

    (3 pts) 2. (a)

  Solution: We want $n\ge 0$ such that $n^2+6n+5$ is a perfect square. Rewrite

  $$n^2+6n+5={(n+3)}^2-4.$$

  Let ${(n+3)}^2-4=m^2$, so

  $${(n+3)}^2-m^2=4⟹(n+3-m)(n+3+m)=4.$$

  The integer factor pairs of $4$ are $(1,4)$, $(2,2)$, $(-1,-4)$, $(-2,-2)$. Solving $n$ from $a=n+3-m$, $b=n+3+m$, each gives either a noninteger $n$ or . Thus no $n\ge 0$ works. Therefore the answer is $0$.

• 3.

  Let $P(x)$ be a nonzero polynomial satisfying

  $$(x^3+3x^2+3x+2)P(x-1)=(x^3-3x^2+3x-2)P(x)$$

  for all real numbers $x.$ Which is the degree of $P(x)\mathrm{?}$

  (a) $2$    (b) $3$    (c) $4$    (d) $5$    (e) $6$

    (3 pts) 3. (e)

  Solution: We can rewrite the above equation as

  $$(x+2)(x^2+x+1)P(x-1)=(x-2)(x^2-x+1)P(x).$$

  ($\ast$)

  Choose $x=2,$ we deduce that $P(1)=0.$ Choose $x=-2$, we deduce that $P(-2)=0.$ Choose $x=-1$, we deduce from the above equation and $P(-2)=0$ that $P(-1)=0$. Choose $x=1$, we deduce from the above equation and $P(1)=0$ that $P(0)=0.$ Therefore, we can find a polynomial $G(x)$ such that

  $$P(x)=x(x-1)(x+1)(x+2)G(x),$$

  which implies from ($\ast$) that

  $$(x^2+x+1)G(x-1)=(x^2-x+1)G(x),$$

  or

  $$\frac{G(x-1)}{{(x-1)}^2+(x-1)+1}=\frac{G(x)}{x^2+x+1},$$

  which implies that $R(x-1)=R(x)$ for all $x$, where $R(x)=G(x)/(x^2+x+1).$ This means that $R(x)$ must be a constant $C$. Thus, $G(x)=C(x^2+x+1),$ which implies that

  $$P(x)=Cx(x-1)(x+1)(x+2)(x^2+x+1).$$

  Hence, the degree of $P(x)$ is $6.$

• 4.

  Two triangles have the same perimeter. The first has side ratios $3:4:5$ and the second has ratios $7:24:25$. What is the ratio of their areas?

  (a) $5:7$   (b) $7:5$    (c) $14:9$    (d) $35:32$    (e) $5:4$

    (3 pts) 4. (c)

  Solution: Let the similar triangles have scale factors $s$ and $t$, so their sides are $3s,4s,5s$ and $7t,24t,25t$. Equal perimeters give

  $$12s=56t⟹s=\frac{14}{3}t.$$

  Both triangles are right triangles, so their areas are

  $$A_1=\frac{1}{2}(3s)(4s)=6s^2,A_2=\frac{1}{2}(7t)(24t)=84t^2.$$

  Thus

  $$\frac{A_1}{A_2}=\frac{6s^2}{84t^2}=\frac{s^2}{14t^2}=\frac{{(14/3)}^2}{14}=\frac{196}{126}=\frac{14}{9}.$$

  Therefore, the ratio of their areas is $14:9$.

• 5.

  Triangle $ABC$ has area $1$. A point $M$ moves along side $BC$. Through $M$, draw a line parallel to $AC$ meeting $AB$ at $D$, and a line parallel to $AB$ meeting $AC$ at $E$. The quadrilateral $ADME$ is a parallelogram. Find the maximum possible area of parallelogram $ADME$.

  (a) $1$     (b) $2$     (c) $1/2$     (d) $3/2$     (e) $3$

    (3 pts) 5. (c)

  Solution:

  

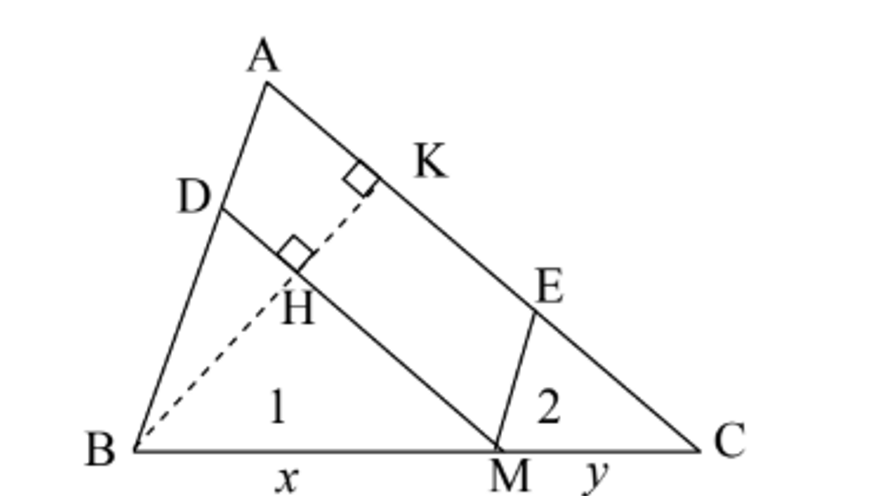
  Maximizing ${\mathrm{S}}_{ADME}$ is equivalent to maximizing the ratio

  $$\frac{{\mathrm{S}}_{ADME}}{{\mathrm{S}}_{ABC}}.$$

  Draw $BK⟂AC$ intersecting $MD$ at $H$. Then

  $${\mathrm{S}}_{ADME}=MD\cdot HK,{\mathrm{S}}_{ABC}=\frac{1}{2}AC\cdot BK,$$

  so

  $$\frac{{\mathrm{S}}_{ADME}}{{\mathrm{S}}_{ABC}}=2\cdot \frac{MD}{AC}\cdot \frac{HK}{BK}.$$

  Let $MB=x$ and $MC=y$. Since $MD\parallel AC$, we have

  $$\frac{MD}{AC}=\frac{BM}{BC}=\frac{x}{x+y},\frac{HK}{BK}=\frac{MC}{BC}=\frac{y}{x+y}.$$

  By the inequality

  $$\frac{xy}{{(x+y)}^2}\le \frac{1}{4}\Rightarrow \frac{S_{ADME}}{S_{ABC}}=\frac{2xy}{{(x+y)}^2}\le \frac{1}{2}.$$

  Equality occurs when $x=y$. Therefore,

  $$\max S_{ADME}=\frac{1}{2}{S}_{ABC}=\frac{1}{2},$$

  which happens when $M$ is the midpoint of $BC$.

• 6.

  A teacher has 300 identical books and wants to pack them into boxes with a different number of books in each box. What is the greatest possible number of boxes?

  (a) $23$    (b) $24$    (c) $25$    (d) $26$    (e) none of these

    (3 pts) 6. (b)

  Solution: Suppose the boxes have sizes $1,2,\mathrm{\dots },k$. Then the total number of books is

  $$1+2+\mathrm{\cdots }+k=\frac{k(k+1)}{2}.$$

  We require $\frac{k(k+1)}{2}\le 300.$ This inequality is equivalent to $k^2+k-600\le 0.$ The positive root of the quadratic equation $k^2+k-600=0$ is $24.$ Thus $k\le 24$. Since

  $$1+2+\mathrm{\cdots }+24=\frac{24\cdot 25}{2}=300,$$

  the value $k=24$ is achievable. For $k=25$, we would need

  $$1+2+\mathrm{\cdots }+25=\frac{25\cdot 26}{2}=325>300,$$

  which is impossible. Therefore, the greatest possible number of boxes is $24$.

• 7.

  How many pairs of integers $(x,y)$ satisfy the equation ${\displaystyle \frac{x^2+y^2}{x+y}}={\displaystyle \frac{85}{13}}$?

  (a) $1$    (b) $2$    (c) $3$    (d) $4$    (e) no integer is satisfied

    (3 pts) 7. (b)

  Solution: We want integers $x,y$ such that

  $$\frac{x^2+y^2}{x+y}=\frac{85}{13},x+y\ne 0.$$

  Cross–multiply:

  $$13(x^2+y^2)=85(x+y).$$

  Let $s=x+y$ and $p=xy$. Then $x^2+y^2=s^2-2p$, so

  $$13(s^2-2p)=85s⟹p=\frac{s(13s-85)}{26}.$$

  For integer solutions, we need an integer $p$ and the discriminant

  $$\mathrm{\Delta }=s^2-4p$$

  to be a nonnegative perfect square. Substitute $p$:

  $$\mathrm{\Delta }=s^2-4\cdot \frac{s(13s-85)}{26}=\frac{s(170-13s)}{13}.$$

  Thus $\mathrm{\Delta }$ is an integer only if $13\mid s$, so write $s=13k$. Then

  $$\mathrm{\Delta }=k(170-169k).$$

  For $\mathrm{\Delta }\ge 0$ we need $k=0$ or $k=1$. The case $k=0$ gives $s=0$, which is not allowed since $x+y\ne 0$. Thus $k=1$, giving $s=13$ and $\mathrm{\Delta }=1$.

  Therefore

  $$x,y=\frac{13\pm 1}{2}\in \{6,7\}.$$

  The integer solutions are $(6,7)$ and $(7,6)$, so the answer is $2$.