3 The Graphical Behavior of Functions 3.2 The Mean Value Theorem 3.4 Concavity and the Second Derivative

3.3 Increasing and Decreasing Functions

Our study of “nice” functions $f$ in this chapter has so far focused on individual points: points where $f$ is maximal/minimal, points where $f\,^{\prime}(x)=0$ or $f\,^{\prime}$ does not exist, and points $c$ where $f\,^{\prime}(c)$ is the average rate of change of $f$ on some interval.

In this section we begin to study how functions behave between special points; we begin studying in more detail the shape of their graphs.

^†^†margin: Figure 3.3.1: A graph of a function

f

used to illustrate the concepts of increasing and decreasing. Λ

We start with an intuitive concept. Given the graph in Figure 3.3.1, where would you say the function is increasing? Decreasing? Even though we have not defined these terms mathematically, one likely answered that $f$ is increasing when $x>1$ and decreasing when $x<1$ . We formally define these terms here.

Definition 3.3.1 Increasing and Decreasing Functions

Let $f$ be a function defined on an interval $I$ .

(a)

$f$ is increasing on $I$ if for every $a<b$ in $I$ , $f(a)\leq f(b)$ .
(b)

$f$ is decreasing on $I$ if for every $a<b$ in $I$ , $f(a)\geq f(b)$ .

A function is strictly increasing when $a<b$ in $I$ implies $f(a)<f(b)$ , with a similar definition holding for strictly decreasing.

Informally, a function is increasing if as $x$ gets larger (i.e., looking left to right) $f(x)$ gets larger.

Our interest lies in finding intervals in the domain of $f$ on which $f$ is either increasing or decreasing. Such information should seem useful. For instance, if $f$ describes the speed of an object, we might want to know when the speed was increasing or decreasing (i.e., when the object was accelerating vs. decelerating). If $f$ describes the population of a city, we should be interested in when the population is growing or declining.

^†^†margin: Figure 3.3.2: Examining the secant line of an increasing function. Λ

There is a nice relationship between the sign of $f\,^{\prime}$ on some interval and whether $f$ is increasing or decreasing on that interval.

First, suppose that $f(x)$ is differentiable and increasing on the interval $(a,b)$ . Then for any c in (a, b) we have

f\,^{\prime}(c)=\lim_{h\to 0}\frac{f(c+h)-f(c)}{h}=\lim_{h\to 0^{+}}\frac{f(c+% h)-f(c)}{h}\geq 0

because $f(c+h)\geq f(c)$ for small $h>0$ . Thus $f\,^{\prime}(c)\geq 0$ for any $c$ in $(a,b)$ .

Conversely, suppose $f\,^{\prime}(c)\geq 0$ for all $c$ in $(a,b)$ . Then for any $s<t$ in $(a,b)$ , $f$ is continuous on $[s,t]$ and differentiable on $(s,t)$ . The Mean Value Theorem (Theorem 3.2.1) then implies that there is a $c$ in $(s,t)$ such that $f(t)-f(s)=f\,^{\prime}(c)(t-s)\geq 0$ because $f\,^{\prime}(c)\geq 0$ and $t-s>0$ . Therefore $f(t)\geq f(s)$ . This means $f$ is increasing on $(a,b)$ .

We’ve now shown that for any $f$ differentiable on $(a,b)$ , $f$ is increasing on $(a,b)$ if and only if $f\,^{\prime}(c)\geq 0$ for all $c$ in $(a,b)$ . Using the same arguments we could show $f$ is decreasing on $(a,b)$ if and only if $f\,^{\prime}(c)\leq 0$ for all $c$ in $(a,b)$ . The following Theorem is now an immediate consequence.

Theorem 3.3.1 Test For Increasing/Decreasing Functions

Let $f$ be a continuous function on $[a,b]$ and differentiable on $(a,b)$ .

(a)

If $f\,^{\prime}(c)\geq 0$ for all $c$ in $(a,b)$ , then $f$ is increasing on $[a,b]$ .
(b)

If $f\,^{\prime}(c)\leq 0$ for all $c$ in $(a,b)$ , then $f$ is decreasing on $[a,b]$ .
(c)

If $f\,^{\prime}(c)=0$ for all $c$ in $(a,b)$ , then $f$ is constant on $[a,b]$ .

Suppose $a$ and $b$ are in $I$ where $f\,^{\prime}(a)>0$ and $f\,^{\prime}(b)<0$ . Then there must be some number $c$ between $a$ and $b$ with $f\,^{\prime}(c)=0$ . If $f\,^{\prime}$ is continuous on $I$ , this is an immediate consequence of the Intermediate Value Theorem. Even if $f\,^{\prime}$ isn’t continuous, such a $c$ must exist as a consequence of Darboux’s Theorem. (For a special case of this theorem see Exercise 39..) In either case, this leads us to the following method for finding intervals on which a function is increasing or decreasing.

Key Idea 3.3.1 Finding Intervals on which $f$ is Increasing or Decreasing

Let $f$ be a continuous function on an interval I. To find intervals on which $f$ is increasing and decreasing:

(a)

Find the critical points of $f$ . That is, find all $c$ in $I$ where $f\,^{\prime}(c)=0$ or $f\,^{\prime}$ is not defined.
(b)

Use the critical points to divide $I$ into subintervals.
(c)
Pick any point $p$ in each subinterval, and find the sign of $f\,^{\prime}(p)$ .
1. (a)
  
  If $f\,^{\prime}(p)>0$ , then $f$ is increasing on that subinterval.
2. (b)
  
  If $f\,^{\prime}(p)<0$ , then $f$ is decreasing on that subinterval.

Watch the video:
Finding Intervals of Increase / Decrease Local Max / Mins from https://youtu.be/-W4d0qFzyQY

We demonstrate using Key Idea 3.3.1 in the following example.

Example 3.3.1 Finding intervals of increasing/decreasing

Let $f(x)=x^{3}+x^{2}-x+1$ . Find intervals on which $f$ is increasing or decreasing.

SolutionUsing Key Idea 3.3.1, we first find the critical points of $f$ . We have $f\,^{\prime}(x)=3x^{2}+2x-1=(3x-1)(x+1)$ , so $f\,^{\prime}(x)=0$ when $x=-1$ and when $x=1/3$ . We see that $f\,^{\prime}$ is never undefined.

Since an interval was not specified for us to consider, we consider the entire domain of $f$ which is $(-\infty,\infty)$ . We thus break the whole real line into three subintervals based on the two critical points we just found: $(-\infty,-1)$ , $(-1,1/3)$ and $(1/3,\infty)$ . This is shown in the following sign chart.

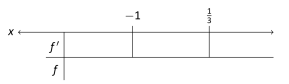
We now pick a value $p$ in each subinterval and find the sign of $f\,^{\prime}(p)$ . All we care about is the sign, so we do not actually have to fully compute $f\,^{\prime}(p)$ ; pick “nice” values that make this simple.

Subinterval 1,: $(-\infty,-1)$ : We (arbitrarily) pick $p=-2$ . We can compute $f\,^{\prime}(-2)$ directly: $f\,^{\prime}(-2)=3(-2)^{2}+2(-2)-1=7>0$ . We conclude that $f$ is increasing on $(-\infty,-1]$ .

Note we can arrive at the same conclusion without computation. For instance, we could choose $p=-100$ . The first term in $f\,^{\prime}(-100)$ , i.e., $3(-100)^{2}$ is clearly positive and very large. The other terms are small in comparison, so we know $f\,^{\prime}(-100)>0$ . All we need is the sign.
Subinterval 2,: $(-1,1/3)$ : We pick $p=0$ since that value seems easy to deal with and note that $f\,^{\prime}(0)=-1<0$ . We conclude $f$ is decreasing on $[-1,1/3]$ .
Subinterval 3,: $(1/3,\infty)$ : Pick an arbitrarily large value for $p>1/3$ and note that $f\,^{\prime}(p)=3p^{2}+2p-1>0$ . We conclude that $f$ is increasing on $[1/3,\infty)$ and use all of our information to complete our sign chart.

^†^†margin: Figure 3.3.3: A graph of

f(x)

in Example 3.3.1, showing where

f

is increasing and decreasing. Λ

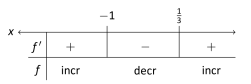
We can verify our calculations by considering Figure 3.3.3, where we have graphed $f$ and $f\,^{\prime}$ . Note how $f\,^{\prime}>0$ when $f$ is increasing and $f\,^{\prime}<0$ when $f$ is decreasing.

One is justified in wondering why so much work is done when the graph seems to make the intervals very clear. We give three reasons why the above work is worthwhile.

First, the points at which $f$ switches from increasing to decreasing are not precisely known given a graph. The graph shows us something significant happens near $x=-1$ and $x=0.3$ , but we cannot determine exactly where from the graph.

One could argue that just finding critical points is important; once we know the significant points are $x=-1$ and $x=1/3$ , the graph shows the increasing/decreasing traits just fine. That is true. However, the technique prescribed here helps reinforce the relationship between increasing/decreasing and the sign of $f\,^{\prime}$ . Once mastery of this concept (and several others) is obtained, one finds that either (a) just the critical points and values are computed and the graph shows all else that is desired, or (b) a graph is never produced, because determining increasing/decreasing using $f\,^{\prime}$ is straightforward and the graph is unnecessary. So our second reason why the above work is worthwhile is this: once mastery of a subject is gained, one has options for finding needed information. We are working to develop mastery.

Finally, our third reason: many problems we face “in the real world” are very complex. Solutions are tractable only through the use of computers to do many calculations for us. Computers do not solve problems “on their own,” however; they need to be taught (i.e., programmed) to do the right things. It would be beneficial to give a function to a computer and have it return maximum and minimum values, intervals on which the function is increasing and decreasing, the locations of relative maxima, etc. The work that we are doing here is easily programmable. It is hard to teach a computer to “look at the graph and see if it is going up or down.” It is easy to teach a computer to “determine if a number is greater than or less than 0.”

In Section 3.1 we learned the definition of relative maxima and minima and found that they occur at critical points. We are now learning that functions can switch from increasing to decreasing (and vice-versa) at critical points. This new understanding of increasing and decreasing creates a great method of determining whether a critical point corresponds to a maximum, minimum, or neither. Imagine a function increasing until a critical point at $x=c$ , after which it decreases. A quick sketch helps confirm that $f(c)$ must be a relative maximum. A similar statement can be made for relative minimums, see Figure 3.3.4. We formalize this concept in a theorem.

^†^†margin: Case 1 Case 2 Case 3 Case 4 Figure 3.3.4: The four cases ofTheorem 3.3.2 Λ

Theorem 3.3.2 First Derivative Test

Suppose that $f$ is continuous on an open interval containing $c$ , differentiable on an open interval containing $c$ except possibly at $c$ , and $c$ is a critical point of $f$ . Then

(a)

If the sign of $f\,^{\prime}$ switches from positive to negative at $c$ , then $f(c)$ is a relative maximum of $f$ .
(b)

If the sign of $f\,^{\prime}$ switches from negative to positive at $c$ , then $f(c)$ is a relative minimum of $f$ .
(c)

If the sign of $f\,^{\prime}$ is positive before and after $c$ , then $f(c)$ is not a relative extrema of $f$ .
(d)

If the sign of $f\,^{\prime}$ is negative before and after $c$ , then $f(c)$ is not a relative extrema of $f$ .

Example 3.3.2 Using the First Derivative Test

Find the intervals on which $f$ is increasing and decreasing, and use the First Derivative Test to determine the relative extrema of $f$ , where

f(x)=\frac{x^{2}+3}{x-1}.

SolutionWe start by noting the domain of $f$ : $(-\infty,1)\cup(1,\infty)$ . Key Idea 3.3.1 describes how to find intervals where $f$ is increasing and decreasing when the domain of $f$ is an interval. Since the domain of $f$ in this example is the union of two intervals, we apply the techniques of Key Idea 3.3.1 to both intervals of the domain of $f$ .

Since $f$ is not defined at $x=1$ , the increasing/decreasing nature of $f$ could switch at this value. We do not formally consider $x=1$ to be a critical point of $f$ , but we will include it in our list of critical points that we find next.

Using the Quotient Rule, we find

f\,^{\prime}(x)=\frac{x^{2}-2x-3}{(x-1)^{2}}.

We need to find the critical points of $f$ ; we want to know when $f\,^{\prime}(x)=0$ and when $f\,^{\prime}$ is not defined. That latter is straightforward: when the denominator of $f\,^{\prime}(x)$ is 0, $f\,^{\prime}$ is undefined. That occurs when $x=1$ , which we’ve already recognized as an important value.

$f\,^{\prime}(x)=0$ when the numerator of $f\,^{\prime}(x)$ is 0. That occurs when $x^{2}-2x-3=(x-3)(x+1)=0$ ; i.e., when $x=-1,3$ .

We have found that $f$ has two critical points, $x=-1,3$ , and at $x=1$ something important might also happen. These three numbers divide the real number line into 4 subintervals:

(-\infty,-1),\quad(-1,1),\quad(1,3)\quad\text{and}\quad(3,\infty).

Pick a number $p$ from each subinterval and test the sign of $f\,^{\prime}$ at $p$ to determine whether $f$ is increasing or decreasing on that interval. Again, we do well to avoid complicated computations; notice that the denominator of $f\,^{\prime}$ is always positive so we can ignore it during our work.

Interval 1,: $(-\infty,-1)$ : Choosing a very small number (i.e., a negative number with a large magnitude) $p$ returns $p^{2}-2p-3$ in the numerator of $f\,^{\prime}$ ; that will be positive. Hence $f$ is increasing on $(-\infty,-1]$ .
Interval 2,: $(-1,1)$ : Choosing 0 seems simple: $f\,^{\prime}(0)=-3<0$ . We conclude $f$ is decreasing on $[-1,1)$ .
Interval 3,: $(1,3]$ : Choosing 2 seems simple: $f\,^{\prime}(2)=-3<0$ . Again, $f$ is decreasing.
Interval 4,: $(3,\infty)$ : Choosing a very large number $p$ from this subinterval will give a positive numerator and (of course) a positive denominator. So $f$ is increasing on $[3,\infty)$ .

In summary, $f$ is increasing on $(-\infty,-1]$ and $[3,\infty)$ and is decreasing on $[-1,1)$ and $(1,3]$ . Since at $x=-1$ , the sign of $f\,^{\prime}$ switched from positive to negative, Theorem 3.3.2 states that $f(-1)$ is a relative maximum of $f$ . At $x=3$ , the sign of $f\,^{\prime}$ switched from negative to positive, meaning $f(3)$ is a relative minimum. At $x=1$ , $f$ is not defined, so there is no relative extrema at $x=1$ .

^†^†margin: Note: We will use “U” in our sign charts to indicate that something is undefined. Λ

^†^†margin: Figure 3.3.5: A graph of

f(x)

in Example 3.3.2, showing where

f

is increasing and decreasing. Λ

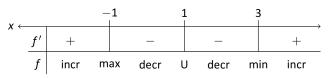
This is summarized in the number line shown above. Also, Figure 3.3.5 shows a graph of $f$ , confirming our calculations. This figure also shows $f\,^{\prime}$ , again demonstrating that $f$ is increasing when $f\,^{\prime}>0$ and decreasing when $f\,^{\prime}<0$ .

One is often tempted to think that functions always alternate “increasing, decreasing, increasing, decreasing, …” around critical points. Our previous example demonstrated that this is not always the case. While $x=1$ was not technically a critical point, it was an important value we needed to consider. We found that $f$ was decreasing on “both sides of $x=1$ .”

Example 3.3.3 Using the First Derivative Test

Find the intervals on which $f(x)=x^{8/3}-4x^{2/3}$ is increasing and decreasing and identify the relative extrema.

SolutionWe again start with taking derivatives. Since we know we want to solve $f\,^{\prime}(x)=0$ , we will do some algebra after taking derivatives.

	$\displaystyle f(x)$	$\displaystyle=x^{\frac{8}{3}}-4x^{\frac{2}{3}}$
	$\displaystyle f\,^{\prime}(x)$	$\displaystyle=\frac{8}{3}x^{\frac{5}{3}}-\frac{8}{3}x^{-\frac{1}{3}}$
		$\displaystyle=\frac{8}{3}x^{-\frac{1}{3}}\left(x^{\frac{6}{3}}-1\right)$
		$\displaystyle=\frac{8}{3}x^{-\frac{1}{3}}(x^{2}-1)$
		$\displaystyle=\frac{8}{3}x^{-\frac{1}{3}}(x-1)(x+1).$

This derivation of $f\,^{\prime}$ shows that $f\,^{\prime}(x)=0$ when $x=\pm 1$ and $f\,^{\prime}$ is not defined when $x=0$ . Thus we have 3 critical points, breaking the number line into 4 subintervals: $(-\infty,-1)$ , $(-1,0)$ , $(0,1)$ , and $(1\infty)$ .

Interval 1,

$(\infty,-1)$ : We choose $p=-2$ ; we can easily verify that $f\,^{\prime}(-2)<0$ . So $f$ is decreasing on $(-\infty,-1]$ .

Interval 2,

$(-1,0)$ : Choose $p=-1/2$ . Once more we practice finding the sign of $f\,^{\prime}(p)$ without computing an actual value. We have $f\,^{\prime}(p)=(8/3)p^{-1/3}(p-1)(p+1)$ ; find the sign of each of the three terms.

f\,^{\prime}(p)=\frac{8}{3}\cdot\underbrace{p^{-\frac{1}{3}}}_{<0}\cdot% \underbrace{(p-1)}_{<0}\underbrace{(p+1)}_{>0}.

We have a “negative $\times$ negative $\times$ positive” giving a positive number; $f$ is increasing on $[-1,0]$ .

Interval 3,

$(0,1)$ : We do a similar sign analysis as before, using $p$ in $(0,1)$ .

f\,^{\prime}(p)=\frac{8}{3}\cdot\underbrace{p^{-\frac{1}{3}}}_{>0}\cdot% \underbrace{(p-1)}_{<0}\underbrace{(p+1)}_{>0}.

We have 2 positive factors and one negative factor; $f\,^{\prime}(p)<0$ and so $f$ is decreasing on $[0,1]$ .

Interval 4,

$(1,\infty)$ : Similar work to that done for the other three intervals shows that $f\,^{\prime}(x)>0$ on $(1,\infty)$ , so $f$ is increasing on $[1,\infty)$ . We can now put all this information into a chart.

^†^†margin: Figure 3.3.6: A graph of

f(x)

in Example 3.3.3, showing where

f

is increasing and decreasing. Λ

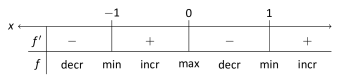
We conclude by stating that $f$ is increasing on $(-1,0)$ and $(1,\infty)$ and decreasing on $(-\infty,-1)$ and $(0,1)$ . The sign of $f\,^{\prime}$ changes from negative to positive around $x=-1$ and $x=1$ , meaning by Theorem 3.3.2 that $f(-1)$ and $f(1)$ are relative minima of $f$ . As the sign of $f\,^{\prime}$ changes from positive to negative at $x=0$ , we have a relative maximum at $f(0)$ . Figure 3.3.6 shows a graph of $f$ , confirming our result. We also graph $f\,^{\prime}$ , highlighting once more that $f$ is increasing when $f\,^{\prime}>0$ and is decreasing when $f\,^{\prime}<0$ .

We examine one more example.

Example 3.3.4 Using the First Derivative Test with Trigonometry

Find the intervals on which $f(\theta)=\cos\theta-\cos^{2}\theta$ is increasing and decreasing and find the relative extrema on the interval $[0,2\pi]$ .

SolutionWe see that $f\,^{\prime}(\theta)=-\sin\theta+2\cos\theta\sin\theta=\sin\theta(2\cos\theta-1)$ . Therefore, $f\,^{\prime}(\theta)=0$ when $\theta=0,\frac{\pi}{3},\pi,\frac{5\pi}{3},2\pi$ . This breaks our number line into four intervals.

Interval 1,: $(0,\frac{\pi}{3})$ : We choose $\theta=\frac{\pi}{6}$ , and see that $\sin\theta$ and $2\cos\theta-1$ are both positive. Therefore, $f\,^{\prime}>0$ .
Interval 2,: $(\frac{\pi}{3},\pi)$ : When $\theta=\frac{\pi}{2}$ , $\sin\theta$ is positive, but $2\cos\theta-1$ is negative. Therefore, $f\,^{\prime}<0$ .
Interval 3,: $(\pi,\frac{5\pi}{3})$ : When $\theta=\frac{3\pi}{2}$ , $\sin\theta$ and $2\cos\theta-1$ are both negative. Therefore, $f\,^{\prime}>0$ .
Interval 4,: $(\frac{5\pi}{3},2\pi)$ : When $\theta=\frac{5\pi}{6}$ , $\sin\theta<0$ and $2\cos\theta-1>0$ so that $f\,^{\prime}<0$ . We summarize this information in a chart.

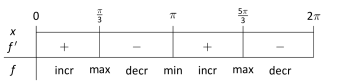
This means that $f$ is increasing on $[0,\frac{\pi}{3}]$ and $[\pi,\frac{5\pi}{3}]$ and decreasing on $[\frac{\pi}{3},\pi]$ and $[\frac{5\pi}{3},2\pi]$ , so that the relative maxima are $f(\frac{\pi}{3})$ and $f(\frac{5\pi}{3})$ and the relative minimum is $f(\pi)$ . (The values $f(0)$ and $f(2\pi)$ would also be relative minima, but relative extrema are not allowed to occur at the endpoints of an interval.)

We have seen how the first derivative of a function helps determine when the function is going “up” or “down.” In the next section, we will see how the second derivative helps determine how the graph of a function curves.

Exercises 3.3

Terms and Concepts

1.

In your own words describe what it means for a function to be increasing.
2.

What does a decreasing function “look like”?
3.

Sketch a graph of a function on $[0,2]$ that is increasing but not strictly increasing.
4.

Give an example of a function describing a situation where it is “bad” to be increasing and “good” to be decreasing.
5.

T/F: Functions always switch from increasing to decreasing, or decreasing to increasing, at critical points.
6.

A function $f$ has derivative $f\,^{\prime}(x)=(\sin x+2)e^{x^{2}+1}$ , where $f\,^{\prime}(x)>1$ for all $x$ . Is $f$ increasing, decreasing, or can we not tell from the given information?

Problems

7.
Given the graph of $f$ , identify the intervals of increasing and decreasing as well as the $x$ coordinates of the relative extrema.
8.
Given the graph of $f$ , identify the intervals of increasing and decreasing as well as the $x$ coordinates of the relative extrema.
9.
Given the graph of $f\,^{\prime}$ , identify the intervals of increasing and decreasing as well as the $x$ coordinates of the relative extrema.
10.
Given the graph of $f\,^{\prime}$ , identify the intervals of increasing and decreasing as well as the $x$ coordinates of the relative extrema.

In Exercises 11–18., a function $f(x)$ is given.

(a)

Compute $f\,^{\prime}(x)$ .
(b)

Graph $f$ and $f\,^{\prime}$ on the same axes (using technology is permitted) and verify Theorem 3.3.1.

11.

$f(x)=2x+3$
12.

$f(x)=x^{2}-3x+5$
13.

$f(x)=\cos x$
14.

$f(x)=\tan x$
15.

$f(x)=x^{3}-5x^{2}+7x-1$
16.

$f(x)=2x^{3}-x^{2}+x-1$
17.

$f(x)=x^{4}-5x^{2}+4$
18.

$\displaystyle f(x)=\frac{1}{x^{2}+1}$

In Exercises 19–38., a function $f(x)$ is given.

(a)

Give the domain of $f$ .
(b)

Find the critical numbers of $f$ .
(c)

Create a number line to determine the intervals on which $f$ is increasing and decreasing.
(d)

Use the First Derivative Test to determine whether each critical point corresponds to a relative maximum, minimum, or neither.

19.

$\displaystyle f(x)=x^{2}+2x-3$
20.

$\displaystyle f(x)=x^{3}+3x^{2}+3$
21.

$\displaystyle f(x)=2x^{3}+x^{2}-x+3$
22.

$\displaystyle f(x)=x^{3}-3x^{2}+3x-1$
23.

$\displaystyle f(x)=\frac{1}{x^{2}-2x+2}$
24.

$\displaystyle f(x)=\frac{x^{2}-4}{x^{2}-1}$
25.

$\displaystyle f(x)=\frac{x}{x^{2}-2x-8}$
26.

$\displaystyle f(x)=\frac{(x-2)^{2/3}}{x}$
27.

$\displaystyle f(x)=\sin x\cos x$ on $(-\pi,\pi)$ .
28.

$\displaystyle f(x)=x^{5}-5x$
29.

$\displaystyle f(x)=x-2\sin x$ on $0\leq x\leq 3\pi$
30.

$\displaystyle f(x)=\cos^{2}x-2\sin x$ on $0\leq x\leq 2\pi$
31.

$\displaystyle f(x)=x\sqrt{x-3}$
32.

$\displaystyle f(x)=(x^{2}-1)^{3}$
33.

$f(x)=x^{1/3}(x+4)$
34.

$f(\theta)=2\cos\theta+\cos^{2}\theta$ on $[0,2\pi]$
35.

$f(x)=2\sqrt{x}-4x^{2}$
36.

$f(x)=5x^{2/3}-2x^{5/3}$
37.

$f(x)=\sin^{3}x$ on $[0,2\pi]$
38.

$f(x)=(x+1)^{5}-5x-2$

39.

A special case of Darboux’s Theorem. Suppose $f(x)$ is differentiable on the open interval $(a,b)$ . Suppose $c$ and $d$ belong to the interval $(a,b)$ with $c<d$ . Show that if $f\,^{\prime}(c)$ and $f\,^{\prime}(d)$ have opposite signs then there is an $r$ in the interval $(c,d)$ such that $f\,^{\prime}(r)=0$ . (This statement would follow from the Intermediate Value Theorem if $f\,^{\prime}$ were continuous on $[a,b]$ but we are not assuming $f\,^{\prime}$ is continuous here.)

Review

40.

Consider $f(x)=x^{2}-3x+5$ on $[-1,2]$ ; find $c$ guaranteed by the Mean Value Theorem.
41.

Consider $f(x)=\sin x$ on $[-\pi/2,\pi/2]$ ; find $c$ guaranteed by the Mean Value Theorem.

3.3 Increasing and Decreasing Functions

Definition 3.3.1 Increasing and Decreasing Functions

Theorem 3.3.1 Test For Increasing/Decreasing Functions

Key Idea 3.3.1 Finding Intervals on which f is Increasing or Decreasing

Example 3.3.1 Finding intervals of increasing/decreasing

Theorem 3.3.2 First Derivative Test

Example 3.3.2 Using the First Derivative Test

Example 3.3.3 Using the First Derivative Test

Example 3.3.4 Using the First Derivative Test with Trigonometry

Exercises 3.3

Terms and Concepts

Problems

Review

Key Idea 3.3.1 Finding Intervals on which $f$ is Increasing or Decreasing