10 Curves in the Plane 10.2 Parametric Equations 10.4 Introduction to Polar Coordinates

10.3 Calculus and Parametric Equations

The previous section defined curves based on parametric equations. In this section we’ll employ the techniques of calculus to study these curves.

We are still interested in lines tangent to points on a curve. They describe how the $y$ -values are changing with respect to the $x$ -values, they are useful in making approximations, and they indicate instantaneous direction of travel.

The slope of the tangent line is still $\frac{dy}{dx}$ , and the Chain Rule allows us to calculate this in the context of parametric equations. If $x=f(t)$ and $y=g(t)$ , the Chain Rule states that

\frac{dy}{dt}=\frac{dy}{dx}\cdot\frac{dx}{dt}.

Solving for $\frac{dy}{dx}$ , we get

\frac{dy}{dx}=\frac{dy/dt}{dx/dt}=\frac{g\hskip 0.75pt^{\prime}(t)}{f\,^{% \prime}(t)},

provided that $f\,^{\prime}(t)\neq 0$ . This is important so we label it a Key Idea.

Key Idea 10.3.1 Finding $\frac{dy}{dx}$ with Parametric Equations.

Let $x=f(t)$ and $y=g(t)$ , where $f$ and $g$ are differentiable on some open interval $I$ and $f\,^{\prime}(t)\neq 0$ on $I$ . Then

\frac{dy}{dx}=\frac{dy/dt}{dx/dt}=\frac{g\hskip 0.75pt^{\prime}(t)}{f\,^{% \prime}(t)}.

We use this to define the tangent line.

Definition 10.3.1 Tangent Lines

Let a curve $C$ be parameterized by $x=f(t)$ and $y=g(t)$ , where $f$ and $g$ are differentiable functions on some interval $I$ containing $t=t_{0}$ . The tangent line to $C$ at $t=t_{0}$ is the line through $(f(t_{0}),g(t_{0}))$ with slope $m=\frac{g^{\prime}(t_{0})}{f\,^{\prime}(t_{0})}$ , provided $f\,^{\prime}(t_{0})\neq 0$ .

It is possible for parametric curves to have horizontal and vertical tangents. As expected a horizontal tangent occurs whenever $\frac{dy}{dx}=0$ or when $\frac{dy}{dt}=0$ (provided $\frac{dx}{dt}\neq 0$ ). Similarly, a vertical tangent occurs whenever $\frac{dy}{dx}$ is undefined or when $\frac{dx}{dt}=0$ (provided $\frac{dy}{dt}\neq 0$ ).

Definition 10.3.2 Normal Lines

The normal line to a curve $C$ at a point $P$ is the line through $P$ and perpendicular to the tangent line at $P$ . For $t=t_{0}$ the normal line is the line through $(f(t_{0}),g(t_{0}))$ with slope $m=-\frac{f\,^{\prime}(t_{0})}{g^{\prime}(t_{0})}$ , provided $g^{\prime}(t_{0})\neq 0$ .

As with the tangent line we note that it is possible for a normal line to be vertical or horizontal. A horizontal normal line occurs whenever $\frac{dy}{dx}$ is undefined or when $\frac{dx}{dt}=0$ (provided $\frac{dy}{dt}\neq 0$ ). Similarly, a vertical normal line occurs whenever $\frac{dy}{dx}=0$ or when $\frac{dy}{dt}=0$ (provided $\frac{dx}{dt}\neq 0$ ). In other words, if the curve $C$ has a vertical tangent at $(f(t_{0}),g(t_{0}))$ the normal line will be horizontal and if the tangent is horizontal the normal line will be a vertical line.

Watch the video:
Derivatives of Parametric Functions from https://youtu.be/k5QnaGVk1JI

Example 10.3.1 Tangent and Normal Lines to Curves

Let $x=5t^{2}-6t+4$ and $y=t^{2}+6t-1$ , and let $C$ be the curve defined by these equations.

1.

Find the equations of the tangent and normal lines to $C$ at $t=3$ .
2.

Find where $C$ has vertical and horizontal tangent lines.

Solution

1.

We start by computing $f\,^{\prime}(t)=10t-6$ and $g\hskip 0.75pt^{\prime}(t)=2t+6$ . Thus

$\frac{dy}{dx}=\frac{2t+6}{10t-6}.$

Make note of something that might seem unusual: $\frac{dy}{dx}$ is a function of $t$ , not $x$ . Just as points on the curve are found in terms of $t$ , so are the slopes of the tangent lines.
The point on $C$ at $t=3$ is $(31,26)$ . The slope of the tangent line is $m=1/2$ and the slope of the normal line is $m=-2$ . Thus,
- •
  
  the equation of the tangent line is $\displaystyle y=\frac{1}{2}(x-31)+26$ , and
- •
  
  the equation of the normal line is $\displaystyle y=-2(x-31)+26$ .
This is illustrated in Figure 10.3.1.
^†^†margin: Figure 10.3.1: Graphing tangent and normal lines in Example 10.3.1.
2.

To find where $C$ has a horizontal tangent line, we set $\frac{dy}{dx}=0$ and solve for $t$ . In this case, this amounts to setting $g\hskip 0.75pt^{\prime}(t)=0$ and solving for $t$ (and making sure that $f\,^{\prime}(t)\neq 0$ ).

$g\hskip 0.75pt^{\prime}(t)=0\quad\Rightarrow\quad 2t+6=0\quad\Rightarrow\quad t% =-3.$

The point on $C$ corresponding to $t=-3$ is $(67,-10)$ ; the tangent line at that point is horizontal (hence with equation $y=-10$ ).

To find where $C$ has a vertical tangent line, we find where it has a horizontal normal line, and set $-\frac{f\,^{\prime}(t)}{g\hskip 0.75pt^{\prime}(t)}=0$ . This amounts to setting $f\,^{\prime}(t)=0$ and solving for $t$ (and making sure that $g\hskip 0.75pt^{\prime}(t)\neq 0$ ).

$f\,^{\prime}(t)=0\quad\Rightarrow\quad 10t-6=0\quad\Rightarrow\quad t=0.6.$

The point on $C$ corresponding to $t=0.6$ is $(2.2,2.96)$ . The tangent line at that point is $x=2.2$ .

The points where the tangent lines are vertical and horizontal are indicated on the graph in Figure 10.3.1.

Example 10.3.2 Tangent and Normal Lines to a Circle

1.

Find where the unit circle, defined by $x=\cos t$ and $y=\sin t$ on $[0,2\pi]$ , has vertical and horizontal tangent lines.
2.

Find the equation of the normal line at $t=t_{0}$ .

Solution

1.

We compute the derivative following Key Idea 10.3.1:

$\frac{dy}{dx}=\frac{g\hskip 0.75pt^{\prime}(t)}{f\,^{\prime}(t)}=-\frac{\cos t% }{\sin t}.$

The derivative is $0$ when $\cos t=0$ ; that is, when $t=\pi/2,\ 3\pi/2$ . These are the points $(0,1)$ and $(0,-1)$ on the circle.

The normal line is horizontal (and hence, the tangent line is vertical) when $\sin t=0$ ; that is, when $t=0,\ \pi,\ 2\pi$ , corresponding to the points $(-1,0)$ and $(0,1)$ on the circle. These results should make intuitive sense.
2.

The slope of the normal line at $t=t_{0}$ is $\displaystyle m=\frac{\sin t_{0}}{\cos t_{0}}=\tan t_{0}$ . This normal line goes through the point $(\cos t_{0},\sin t_{0})$ , giving the line

$\displaystyle y$ $\displaystyle=\frac{\sin t_{0}}{\cos t_{0}}(x-\cos t_{0})+\sin t_{0}$

$\displaystyle=(\tan t_{0})x,$

^†^†margin: Figure 10.3.2: Illustrating how a circle’s normal lines pass through its center.
as long as $\cos t_{0}\neq 0$ . It is an important fact to recognize that the normal lines to a circle pass through its center, as illustrated in Figure 10.3.2. Stated in another way, any line that passes through the center of a circle intersects the circle at right angles.

Example 10.3.3 Tangent lines when $\frac{dy}{dx}$ is not defined

Find the equation of the tangent line to the astroid $x=\cos^{3}t$ , $y=\sin^{3}t$ at $t=0$ , shown in Figure 10.3.3. ^†^†margin: Figure 10.3.3: A graph of an astroid.

SolutionWe start by finding $x\hskip 0.75pt^{\prime}(t)$ and $y\hskip 0.75pt^{\prime}(t)$ :

x\hskip 0.75pt^{\prime}(t)=-3\sin t\cos^{2}t,\qquad y\hskip 0.75pt^{\prime}(t)% =3\cos t\sin^{2}t.

Note that both of these are 0 at $t=0$ ; the curve is not smooth at $t=0$ forming a cusp on the graph. Evaluating $\frac{dy}{dx}$ at this point returns the indeterminate form of “0/0”.

We can, however, examine the slopes of tangent lines near $t=0$ , and take the limit as $t\to 0$ .

	$\displaystyle\lim_{t\to 0}\frac{y\hskip 0.75pt^{\prime}(t)}{x\hskip 0.75pt^{% \prime}(t)}$	$\displaystyle=\lim_{t\to 0}\frac{3\cos t\sin^{2}t}{-3\sin t\cos^{2}t}\quad% \text{\small(We can reduce as $t\neq 0$.)}$
		$\displaystyle=\lim_{t\to 0}\left(-\frac{\sin t}{\cos t}\right)$
		$\displaystyle=0.$

We have accomplished something significant. When the derivative $\frac{dy}{dx}$ returns an indeterminate form at $t=t_{0}$ , we can define its value by setting it to be $\displaystyle\lim_{t\to t_{0}}\frac{dy}{dx}$ , if that limit exists. This allows us to find slopes of tangent lines at cusps, which can be very beneficial.

We found the slope of the tangent line at $t=0$ to be 0; therefore the tangent line is $y=0$ , the $x$ -axis.

Concavity

We continue to analyze curves in the plane by considering their concavity; that is, we are interested in $\frac{d^{2}y}{dx^{2}}$ , “the second derivative of $y$ with respect to $x$ .” To find this, we need to find the derivative of $\frac{dy}{dx}$ with respect to $x$ ; that is,

\frac{d^{2}y}{dx^{2}}=\frac{d}{dx}\left[\frac{dy}{dx}\right],

but recall that $\frac{dy}{dx}$ is a function of $t$ , not $x$ , making this computation not straightforward.

To make the upcoming notation a bit simpler, let $h(t)=\frac{dy}{dx}$ . We want $\frac{d}{dx}[h(t)]$ ; that is, we want $\frac{dh}{dx}$ . We again appeal to the Chain Rule. Note:

\frac{dh}{dt}=\frac{dh}{dx}\cdot\frac{dx}{dt}\quad\Rightarrow\quad\frac{dh}{dx% }=\frac{dh/dt}{dx/dt}.

In words, to find $\dfrac{d^{2}y}{dx^{2}}$ , we first take the derivative of $\dfrac{dy}{dx}$ with respect to $t$ , then divide by $x\hskip 0.75pt^{\prime}(t)$ . We restate this as a Key Idea.

Key Idea 10.3.2 Finding $\frac{d^{2}y}{dx^{2}}$ with Parametric Equations

Let $x=f(t)$ and $y=g(t)$ be twice differentiable functions on an open interval $I$ , where $f\,^{\prime}(t)\neq 0$ on $I$ . Then

\frac{d^{2}y}{dx^{2}}\quad=\quad\frac{\dfrac{d}{dt}\left[\dfrac{dy}{dx}\right]% }{\dfrac{dx}{dt}}\quad=\quad\frac{\dfrac{d}{dt}\left[\dfrac{dy}{dx}\right]}{f% \,^{\prime}(t)}.

Examples will help us understand this Key Idea.

Example 10.3.4 Concavity of Plane Curves

Let $x=5t^{2}-6t+4$ and $y=t^{2}+6t-1$ as in Example 10.3.1. Determine the $t$ -intervals on which the graph is concave up/down.

SolutionConcavity is determined by the second derivative of $y$ with respect to $x$ , $\frac{d^{2}y}{dx^{2}}$ , so we compute that here following Key Idea 10.3.2.

In Example 10.3.1, we found $\displaystyle\frac{dy}{dx}=\frac{2t+6}{10t-6}$ and $f\,^{\prime}(t)=10t-6$ . So:

	$\displaystyle\frac{d^{2}y}{dx^{2}}$	$\displaystyle=\frac{\frac{d}{dt}\left[\frac{2t+6}{10t-6}\right]}{10t-6}$
		$\displaystyle=\frac{-\frac{72}{(10t-6)^{2}}}{10t-6}$
		$\displaystyle=-\frac{72}{(10t-6)^{3}}$
		$\displaystyle=-\frac{9}{(5t-3)^{3}}$

^†^†margin: Figure 10.3.4: Graphing the parametric equations in Example 10.3.4 to demonstrate concavity.

The graph of the parametric functions is concave up when $\frac{d^{2}y}{dx^{2}}>0$ and concave down when $\frac{d^{2}y}{dx^{2}}<0$ . We determine the intervals when the second derivative is greater/less than 0 by first finding when it is 0 or undefined.

As the numerator of $\displaystyle-\frac{9}{(5t-3)^{3}}$ is never 0, $\frac{d^{2}y}{dx^{2}}\neq 0$ for all $t$ . It is undefined when $5t-3=0$ ; that is, when $t=3/5$ . Following the work established in Section 3.4, we look at values of $t$ greater or less than $3/5$ on a number line:

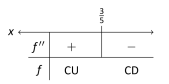
Reviewing Example 10.3.1, we see that when $t=3/5=0.6$ , the graph of the parametric equations has a vertical tangent line. This point is also a point of inflection for the graph, illustrated in Figure 10.3.4.

Example 10.3.5 Concavity of Plane Curves

Find the points of inflection of the graph of the parametric equations $x=\sqrt{t}$ , $y=\sin t$ , for $0\leq t\leq 16$ .

SolutionWe need to compute $\frac{dy}{dx}$ and $\frac{d^{2}y}{dx^{2}}$ .

	$\displaystyle\frac{dy}{dx}=\frac{y\hskip 0.75pt^{\prime}(t)}{x\hskip 0.75pt^{% \prime}(t)}=\frac{\cos t}{1/(2\sqrt{t})}=2\sqrt{t}\cos t.$
	$\displaystyle\frac{d^{2}y}{dx^{2}}=\frac{\frac{d}{dt}\left[\frac{dy}{dx}\right% ]}{x\hskip 0.75pt^{\prime}(t)}=\frac{\cos t/\sqrt{t}-2\sqrt{t}\sin t}{1/(2% \sqrt{t})}=2\cos t-4t\sin t.$

The possible points of inflection are found by setting $\frac{d^{2}y}{dx^{2}}=0$ . This is not trivial, as equations that mix polynomials and trigonometric functions generally do not have “nice” solutions.

^†^†margin: (a) (b) Figure 10.3.5: In (a), a graph of

\frac{d^{2}y}{dx^{2}}

, showing where it is approximately 0. In (b), graph of the parametric equations in Example 10.3.5 along with the points of inflection.

In Figure 10.3.5(a) we see a plot of the second derivative. It shows that it has zeros at approximately $t=0.5,\ 3.5,\ 6.5,\ 9.5,\ 12.5$ and $16$ . These approximations are not very good, made only by looking at the graph. Newton’s Method provides more accurate approximations. Accurate to 2 decimal places, we have:

t=0.65,\ 3.29,\ 6.36,\ 9.48,\ 12.61\ \text{and}\ 15.74.

The corresponding points have been plotted on the graph of the parametric equations in Figure 10.3.5(b). Note how most occur near the $x$ -axis, but not exactly on the axis.

Area with Parametric Equations

We will now find a formula for determining the area under a parametric curve given by the parametric equations

x=f(t)\qquad y=g(t).

We will also need to further add in the assumption that the curve is traced out exactly once as t increases from $\alpha$ to $\beta$ . First, recall how to find the area under $y=F(x)$ on $a\leq x\leq b$ :

A=\int_{a}^{b}F(x)\ dx.

Now think of the parametric equation $x=f(t)$ as a substitution in the integral, assuming that $a=f(\alpha)$ and $b=f(\beta)$ for the purposes of this formula. (There is actually no reason to assume that this will always be the case and so we’ll give a corresponding formula later if it’s the opposite case ( $b=f(\alpha)$ and $a=f(\beta)$ ).)

In order to substitute, we’ll need $dx=f\,^{\prime}(t)\ dt$ . Plugging this into the area formula above and making sure to change the limits to their corresponding $t$ values gives us

A=\int_{\alpha}^{\beta}F(f(t))f\,^{\prime}(t)\ dt.

Since we don’t know what $F(x)$ is, we’ll use the fact that

y=F(x)=F(f(t))=g(t)

and arrive at the formula that we want.

Key Idea 10.3.3 Area Under a Parametric Curve

The area under the parametric curve given by $x=f(t)$ , $y=g(t)$ , for $f(\alpha)=a<x<b=f(\beta)$ is

A=\int_{\alpha}^{\beta}g(t)f\,^{\prime}(t)\ dt.

On the other hand, if we should happen to have $b=f(\alpha)$ and $a=f(\beta)$ , then the formula would be

A=\int_{\beta}^{\alpha}g(t)f\,^{\prime}(t)\ dt.

Let’s work an example.

Example 10.3.6 Finding the area under a parametric curve

Determine the area under the cycloid given by the parametric equations

x=6(\theta-\sin\theta)\qquad y=6(1-\cos\theta)\qquad 0\leq\theta\leq 2\pi.

SolutionFirst, notice that we’ve switched the parameter to $\theta$ for this problem. This is to make sure that we don’t get too locked into always having $t$ as the parameter.

Now, we could graph this to verify that the curve is traced out exactly once for the given range if we wanted to.

There really isn’t too much to this example other than plugging the parametric equations into the formula. We’ll first need the derivative of the parametric equation for $x$ however.

\frac{dx}{d\theta}=6(1-\cos\theta).

The area is then

	$\displaystyle A$	$\displaystyle=\int_{0}^{2\pi}36(1-\cos\theta)^{2}\ d\theta$
		$\displaystyle=36\int_{0}^{2\pi}1-2\cos\theta+\cos^{2}\theta\ d\theta$
		$\displaystyle=36\int_{0}^{2\pi}\frac{3}{2}-2\cos\theta+\frac{1}{2}\cos(2\theta% )\ d\theta$
		$\displaystyle=36\left[\frac{3}{2}\theta-2\sin\theta+\frac{1}{4}\sin(2\theta)% \right]_{0}^{2\pi}$
		$\displaystyle=108\pi.$

Arc Length

We continue our study of the features of the graphs of parametric equations by computing their arc length.

Recall in Section 10.1 we found the arc length of the graph of a function, from $x=a$ to $x=b$ , to be

L=\int_{a}^{b}\sqrt{1+\left(\frac{dy}{dx}\right)^{2}}\ dx.

We can use this equation and convert it to the parametric equation context. Letting $x=f(t)$ and $y=g(t)$ , we know that $\frac{dy}{dx}=g\hskip 0.75pt^{\prime}(t)/f\,^{\prime}(t)$ . Suupose that $f^{\prime}(t)>0$ , and calculate the differential of $x$ :

dx=f\,^{\prime}(t)dt\qquad\Rightarrow\qquad dt=\frac{1}{f\,^{\prime}(t)}\cdot dx.

Starting with the arc length formula above, consider:

	$\displaystyle L$	$\displaystyle=\int_{a}^{b}\sqrt{1+\left(\frac{dy}{dx}\right)^{2}}\ dx$
		$\displaystyle=\int_{a}^{b}\sqrt{1+\frac{[g\hskip 0.75pt^{\prime}(t)]^{2}}{[f\,% ^{\prime}(t)]^{2}}}\ dx$
		$\displaystyle=\int_{a}^{b}\sqrt{[f\,^{\prime}(t)]^{2}+[g\hskip 0.75pt^{\prime}% (t)]^{2}}\cdot\underbrace{\frac{1}{f\,^{\prime}(t)}\ dx}_{=dt}\qquad\text{% Factor out the $[f\,^{\prime}(t)]^{2}$}$
		$\displaystyle=\int_{t_{1}}^{t_{2}}\sqrt{[f\,^{\prime}(t)]^{2}+[g\hskip 0.75pt^% {\prime}(t)]^{2}}\ dt.$

Note the new bounds (no longer “ $x$ ” bounds, but “ $t$ ” bounds). They are found by finding $t_{1}$ and $t_{2}$ such that $a=f(t_{1})$ and $b=f(t_{2})$ . This formula holds even when $f^{\prime}$ isn’t positive and we restate it as a theorem.

Theorem 10.3.1 Arc Length of Parametric Curves

Let $x=f(t)$ and $y=g(t)$ be parametric equations with $f\,^{\prime}$ and $g\hskip 0.75pt^{\prime}$ continuous on some open interval $I$ containing $t_{1}$ and $t_{2}$ on which the graph traces itself only once. The arc length of the graph, from $t=t_{1}$ to $t=t_{2}$ , is

L=\int_{t_{1}}^{t_{2}}\sqrt{[f\,^{\prime}(t)]^{2}+[g\hskip 0.75pt^{\prime}(t)]% ^{2}}\ dt.

As before, these integrals are often not easy to compute. We start with a simple example, then give another where we approximate the solution.

Example 10.3.7 Arc Length of a Circle

Find the arc length of the circle parameterized by $x=3\cos t$ , $y=3\sin t$ on $[0,3\pi/2]$ .

SolutionBy direct application of Theorem 10.3.1, we have

	$\displaystyle L$	$\displaystyle=\int_{0}^{3\pi/2}\sqrt{(-3\sin t)^{2}+(3\cos t)^{2}}\ dt.$
Apply the Pythagorean Theorem.
		$\displaystyle=\int_{0}^{3\pi/2}3\ dt$
		$\displaystyle=3t\Big{\|}_{0}^{3\pi/2}=9\pi/2.$

This should make sense; we know from geometry that the circumference of a circle with radius 3 is $6\pi$ ; since we are finding the arc length of $3/4$ of a circle, the arc length is $3/4\cdot 6\pi=9\pi/2$ .

Example 10.3.8 Arc Length of a Parametric Curve

The graph of the parametric equations $x=t(t^{2}-1)$ , $y=t^{2}-1$ crosses itself as shown in Figure 10.3.6, forming a “teardrop.” Find the arc length of the teardrop. ^†^†margin: Figure 10.3.6: A graph of the parametric equations in Example 10.3.8, where the arc length of the teardrop is calculated.

SolutionWe can see by the parameterizations of $x$ and $y$ that when $t=\pm 1$ , $x=0$ and $y=0$ . This means we’ll integrate from $t=-1$ to $t=1$ . Applying Theorem 10.3.1, we have

	$\displaystyle L$	$\displaystyle=\int_{-1}^{1}\sqrt{(3t^{2}-1)^{2}+(2t)^{2}}\ dt$
		$\displaystyle=\int_{-1}^{1}\sqrt{9t^{4}-2t^{2}+1}\ dt.$

Unfortunately, the integrand does not have an antiderivative expressible by elementary functions. We turn to numerical integration to approximate its value. Using 4 subintervals, Simpson’s Rule approximates the value of the integral as $2.65051$ . Using a computer, more subintervals are easy to employ, and $n=20$ gives a value of $2.71559$ . Increasing $n$ shows that this value is stable and a good approximation of the actual value.

Surface Area of a Solid of Revolution

Related to the formula for finding arc length is the formula for finding surface area. We can adapt the formula found in Key Idea 10.1.2 from Section 10.1 in a similar way as done to produce the formula for arc length done before.

Key Idea 10.3.4 Surface Area of a Solid of Revolution

Consider the graph of the parametric equations $x=f(t)$ and $y=g(t)$ , where $f\,^{\prime}$ and $g\hskip 0.75pt^{\prime}$ are continuous on an open interval $I$ containing $t_{1}$ and $t_{2}$ on which the graph does not cross itself.

1.

The surface area of the solid formed by revolving the graph about the $x$ -axis is (where $g(t)\geq 0$ on $[t_{1},t_{2}]$ ):

$\text{Surface Area}=2\pi\int_{t_{1}}^{t_{2}}g(t)\sqrt{[f\,^{\prime}(t)]^{2}+[g% \hskip 0.75pt^{\prime}(t)]^{2}}\ dt.$
2.

The surface area of the solid formed by revolving the graph about the $y$ -axis is (where $f(t)\geq 0$ on $[t_{1},t_{2}]$ ):

$\text{Surface Area}=2\pi\int_{t_{1}}^{t_{2}}f(t)\sqrt{[f\,^{\prime}(t)]^{2}+[g% \hskip 0.75pt^{\prime}(t)]^{2}}\ dt.$

^†^†margin:

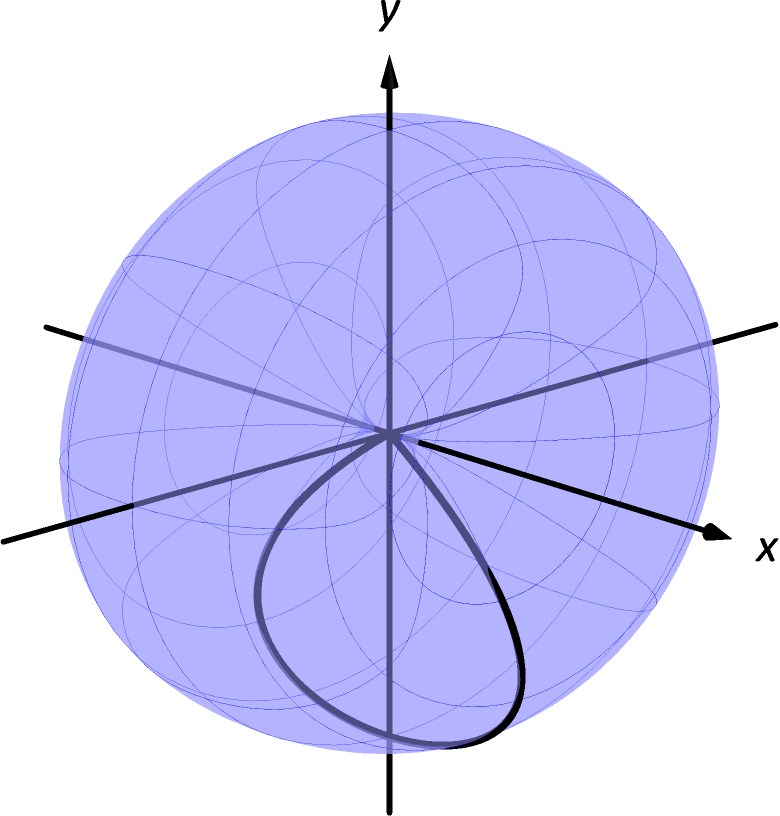Figure 10.3.7: Rotating a teardrop shape about the

x

-axis in Example 10.3.9.

Example 10.3.9 Surface Area of a Solid of Revolution

Consider the teardrop shape formed by the parametric equations $x=t(t^{2}-1)$ , $y=t^{2}-1$ as seen in Example 10.3.8. Find the surface area if this shape is rotated about the $x$ -axis, as shown in Figure 10.3.7.

SolutionThe teardrop shape is formed between $t=-1$ and $t=1$ . Using Key Idea 10.3.4, we see we need for $g(t)\geq 0$ on $[-1,1]$ , and this is not the case. To fix this, we simplify replace $g(t)$ with $-g(t)$ , which flips the whole graph about the $x$ -axis (and does not change the surface area of the resulting solid). The surface area is:

	$\displaystyle\text{Area}\ S$	$\displaystyle=2\pi\int_{-1}^{1}(1-t^{2})\sqrt{(3t^{2}-1)^{2}+(2t)^{2}}\ dt$
		$\displaystyle=2\pi\int_{-1}^{1}(1-t^{2})\sqrt{9t^{4}-2t^{2}+1}\ dt.$

Once again we arrive at an integral that we cannot compute in terms of elementary functions. Using Simpson’s Rule with $n=20$ , we find the area to be $S=9.44$ . Using larger values of $n$ shows this is accurate to 2 places after the decimal.

After defining a new way of creating curves in the plane, in this section we have applied calculus techniques to the parametric equation defining these curves to study their properties. In the next section, we define another way of forming curves in the plane. To do so, we create a new coordinate system, called polar coordinates, that identifies points in the plane in a manner different than from measuring distances from the $y$ - and $x$ - axes.

Exercises 10.3

Terms and Concepts

1.

T/F: Given parametric equations $x=f(t)$ and $y=g(t)$ , $\frac{dy}{dx}=f\,^{\prime}(t)/g^{\prime}(t)$ , as long as $g^{\prime}(t)\neq 0$ .
2.

Given parametric equations $x=f(t)$ and $y=g(t)$ , the derivative $\frac{dy}{dx}$ as given in Key Idea 10.3.1 is a function of ?
3.

T/F: Given parametric equations $x=f(t)$ and $y=g(t)$ , to find $\frac{d^{2}y}{dx^{2}}$ , one simply computes $\frac{d}{dt}\Big{(}\frac{dy}{dx}\Big{)}.$
4.

T/F: If $\frac{dy}{dx}=0$ at $t=t_{0}$ , then the normal line to the curve at $t=t_{0}$ is a vertical line.

Problems

In Exercises 5–12, parametric equations for a curve are given.

(a)

Find $\dfrac{dy}{dx}$ .
(b)

Find the equations of the tangent and normal line(s) at the point(s) given.
(c)

Sketch the graph of the parametric functions along with the found tangent and normal lines.

5.

$x=t$ , $y=t^{2}$ ; $t=1$
6.

$x=\sqrt{t}$ , $y=5t+2$ ; $t=4$
7.

$x=t^{2}-t$ , $y=t^{2}+t$ ; $t=1$
8.

$x=t^{2}-1$ , $y=t^{3}-t$ ; $t=0$ and $t=1$
9.

$x=\sec t$ , $y=\tan t$ on $(-\pi/2,\pi/2)$ ; $t=\pi/4$
10.

$x=\cos t$ , $y=\sin(2t)$ on $[0,2\pi]$ ; $t=\pi/4$
11.

$x=\cos t\sin(2t)$ , $y=\sin t\sin(2t)$ on $[0,2\pi]$ ; $t=3\pi/4$
12.

$x=e^{t/10}\cos t$ , $y=e^{t/10}\sin t$ ; $t=\pi/2$

In Exercises 13–20, find $t$ -values where the curve defined by the given parametric equations has horizontal or vertical tangent lines. Note: these are the same equations as in Exercises 5–12.

13.

$x=t$ , $y=t^{2}$
14.

$x=\sqrt{t}$ , $y=5t+2$
15.

$x=t^{2}-t$ , $y=t^{2}+t$
16.

$x=t^{2}-1$ , $y=t^{3}-t$
17.

$x=\sec t$ , $y=\tan t$ on $(-\pi/2,\pi/2)$
18.

$x=\cos t$ , $y=\sin(2t)$ on $[0,2\pi]$
19.

$x=\cos t\sin(2t)$ , $y=\sin t\sin(2t)$ on $[0,2\pi]$
20.

$x=e^{t/10}\cos t$ , $y=e^{t/10}\sin t$ on $[-\pi,\pi]$

In Exercises 21–24, find $t=t_{0}$ where the graph of the given parametric equations is not smooth, then find $\displaystyle\lim_{t\to t_{0}}\frac{dy}{dx}$ .

21.

$\displaystyle x=\frac{1}{t^{2}+1}$ , $y=t^{3}$
22.

$x=-t^{3}+7t^{2}-16t+13$ , $y=t^{3}-5t^{2}+8t-2$
23.

$x=t^{3}-3t^{2}+3t-1$ , $y=t^{2}-2t+1$
24.

$\displaystyle x=\cos^{2}t$ , $y=1-\sin^{2}t$

In Exercises 25–32, parametric equations for a curve are given. Find $\frac{d^{2}y}{dx^{2}}$ , then determine the intervals on which the graph of the curve is concave up/down. Note: these are the same equations as in Exercises 5–12.

25.

$x=t$ , $y=t^{2}$
26.

$x=\sqrt{t}$ , $y=5t+2$
27.

$x=t^{2}-t$ , $y=t^{2}+t$
28.

$x=t^{2}-1$ , $y=t^{3}-t$
29.

$x=\sec t$ , $y=\tan t$ on $(-\pi/2,\pi/2)$
30.

$x=\cos t$ , $y=\sin(2t)$ on $[0,2\pi]$
31.

$\displaystyle x=\cos t\sin(2t)$ , $y=\sin t\sin(2t)$ on $[-\pi/2,\pi/2]$
32.

$x=e^{t/10}\cos t$ , $y=e^{t/10}\sin t$

In Exercises 33–40, find the arc length of the graph of the parametric equations on the given interval(s).

33.

$x=-3\sin(2t)$ , $y=3\cos(2t)$ on $[0,\pi]$
34.

$x=e^{t/10}\cos t$ , $y=e^{t/10}\sin t$ on $[0,2\pi]$ and $[2\pi,4\pi]$
35.

$x=5t+2$ , $y=1-3t$ on $[-1,1]$
36.

$x=2t^{3/2}$ , $y=3t$ on $[0,1]$
37.

$x=\cos t$ , $y=\sin t$ on $[0,2\pi]$
38.

$x=1+3t^{2}$ , $y=4+2t^{3}$ on $[0,1]$
39.

$x=\dfrac{t}{1+t}$ , $y=\ln(1+t)$ on $[0,2]$
40.

$x=e^{t}-t$ , $y=4e^{-t/2}$ on $[-8,3]$

In Exercises 41–44, numerically approximate the given arc length.

41.

Approximate the arc length of one petal of the rose curve $x=\cos t\cos(2t)$ , $y=\sin t\cos(2t)$ using Simpson’s Rule and $n=4$ .
42.

Approximate the arc length of the “bow tie curve” $x=\cos t$ , $y=\sin(2t)$ using Simpson’s Rule and $n=6$ .
43.

Approximate the arc length of the parabola $x=t^{2}-t$ , $y=t^{2}+t$ on $[-1,1]$ using Simpson’s Rule and $n=4$ .
44.

A common approximate of the circumference of an ellipse given by $x=a\cos t$ , $y=b\sin t$ is $\displaystyle C\approx 2\pi\sqrt{\frac{a^{2}+b^{2}}{2}}$ . Use this formula to approximate the circumference of $x=5\cos t$ , $y=3\sin t$ and compare this to the approximation given by Simpson’s Rule and $n=6$ .

In Exercises 45–50, a solid of revolution is described. Find or approximate its surface area as specified.

45.
Find the surface area of the sphere formed by rotating the circle $x=2\cos t$ , $y=2\sin t$ about: (a) the $x$ -axis and (b) the $y$ -axis.
46.

Find the surface area of the torus (or “donut”) formed by rotating the circle $x=\cos t+2$ , $y=\sin t$ about the $y$ -axis.
47.

Find the surface area of the solid formed by rotating the curve $x=a\cos^{3}\theta$ , $y=a\sin^{3}\theta$ on $[0,\pi/2]$ about the $x-$ axis
48.

Find the surface area of the solid formed by rotating the curve $x=3t^{2}$ , $y=2t^{3}$ on $[0,5]$ about the $y-$ axis
49.

Approximate the surface area of the solid formed by rotating the “upper right half” of the bow tie curve $x=\cos t$ , $y=\sin(2t)$ on $[0,\pi/2]$ about the $x$ -axis, using Simpson’s Rule and $n=4$ .
50.

Approximate the surface area of the solid formed by rotating the one petal of the rose curve $x=\cos t\cos(2t)$ , $y=\sin t\cos(2t)$ on $[0,\pi/4]$ about the $x$ -axis, using Simpson’s Rule and $n=4$ .

	$\displaystyle y$	$\displaystyle=\frac{\sin t_{0}}{\cos t_{0}}(x-\cos t_{0})+\sin t_{0}$
		$\displaystyle=(\tan t_{0})x,$