11 Vectors 11.3 The Dot Product 11.5 Lines

11.4 The Cross Product

“Orthogonality” is immensely important. A quick scan of your current environment will undoubtedly reveal numerous surfaces and edges that are perpendicular to each other (including the edges of this page). The dot product provides a quick test for orthogonality: vectors $\vec{u}$ and $\vec{v}$ are perpendicular if, and only if, $\vec{u}\cdot\vec{v}=0$ .

Given two non-parallel, nonzero vectors $\vec{u}$ and $\vec{v}$ in space, it is very useful to find a vector $\vec{w}$ that is perpendicular to both $\vec{u}$ and $\vec{v}$ . There is a operation, called the cross product, that creates such a vector. This section defines the cross product, then explores its properties and applications.

Definition 11.4.1 Cross Product

Let $\vec{u}=\left\langle u_{1},u_{2},u_{3}\right\rangle$ and $\vec{v}=\left\langle v_{1},v_{2},v_{3}\right\rangle$ be vectors in $\mathbb{R}^{3}$ . The cross product of $\vec{u}$ and $\vec{v}$ , denoted $\vec{u}\times\vec{v}$ , is the vector

\vec{u}\times\vec{v}=\left\langle u_{2}v_{3}-u_{3}v_{2},-(u_{1}v_{3}-u_{3}v_{1% }),u_{1}v_{2}-u_{2}v_{1}\right\rangle.

This definition can be a bit cumbersome to remember. After an example we will give a convenient method for computing the cross product. For now, careful examination of the products and differences given in the definition should reveal a pattern that is not too difficult to remember. (For instance, in the first component only 2 and 3 appear as subscripts; in the second component, only 1 and 3 appear as subscripts. Further study reveals the order in which they appear.)

Watch the video:
Cross Product from https://youtu.be/qsgK1d-_8ik

Let’s practice using this definition by computing a cross product.

Example 11.4.1 Computing a cross product

Let $\vec{u}=\left\langle 2,-1,4\right\rangle$ and $\vec{v}=\left\langle 3,2,5\right\rangle$ . Find $\vec{u}\times\vec{v}$ , and verify that it is orthogonal to both $\vec{u}$ and $\vec{v}$ .

SolutionUsing Definition 11.4.1, we have

\vec{u}\times\vec{v}=\left\langle(-1)5-(4)2,-\big{(}(2)5-(4)3\big{)},(2)2-(-1)% 3\right\rangle=\left\langle-13,2,7\right\rangle.

(We encourage the reader to compute this product on their own, then verify their result.)

We test whether or not $\vec{u}\times\vec{v}$ is orthogonal to $\vec{u}$ and $\vec{v}$ using the dot product:

	$\displaystyle\big{(}\vec{u}\times\vec{v}\big{)}\cdot\vec{u}$	$\displaystyle=\left\langle-13,2,7\right\rangle\cdot\left\langle 2,-1,4\right% \rangle=0,$
	$\displaystyle\big{(}\vec{u}\times\vec{v}\big{)}\cdot\vec{v}$	$\displaystyle=\left\langle-13,2,7\right\rangle\cdot\left\langle 3,2,5\right% \rangle=0.$

Since both dot products are zero, $\vec{u}\times\vec{v}$ is indeed orthogonal to both $\vec{u}$ and $\vec{v}$ .

Additional Material on $2\times 2$ and $3\times 3$ determinants

We will now make a slight digression. Given four numbers $a$ , $b$ , $c$ , $d$ we define the $2\times 2$ determinant

\begin{vmatrix}a&b\\ c&d\end{vmatrix}=ad-bc.

Thus

\begin{vmatrix}1&2\\ 3&4\end{vmatrix}=-2\text{ and }\begin{vmatrix}3&-2\\ -6&4\end{vmatrix}=0.

Given nine numbers $r_{1}$ , $r_{2}$ , $r_{3}$ , $s_{1}$ , $s_{2}$ , $s_{3}$ , $t_{1}$ , $t_{2}$ , $t_{3}$ we define the $3\times 3$ determinant in terms of three $2\times 2$ determinants as follows

\begin{vmatrix}r_{1}&r_{2}&r_{3}\\ s_{1}&s_{2}&s_{3}\\ t_{1}&t_{2}&t_{3}\end{vmatrix}=r_{1}\begin{vmatrix}s_{2}&s_{3}\\ t_{2}&t_{3}\end{vmatrix}\stackrel{{\scriptstyle!}}{{-}}r_{2}\begin{vmatrix}s_{% 1}&s_{3}\\ t_{1}&t_{3}\end{vmatrix}+r_{3}\begin{vmatrix}s_{1}&s_{2}\\ t_{1}&t_{2}\end{vmatrix}.

Note the minus sign in the second term. Thus

	$\displaystyle\begin{vmatrix}1&2&3\\ 0&-1&5\\ 7&4&0\end{vmatrix}$	$\displaystyle=1\begin{vmatrix}-1&5\\ 4&0\end{vmatrix}-2\begin{vmatrix}0&5\\ 7&0\end{vmatrix}+3\begin{vmatrix}0&-1\\ 7&4\end{vmatrix}$
		$\displaystyle=1\cdot(-20)-2\cdot(-35)+3\cdot 7$
		$\displaystyle=71.$

We can now express $\vec{v}\times\vec{w}$ as a symbolic $3\times 3$ determinant as follows.

	$\displaystyle\vec{v}\times\vec{w}$	$\displaystyle=\begin{vmatrix}\vec{\imath}&\vec{\jmath}&\vec{k}\\ a_{1}&a_{2}&a_{3}\\ b_{1}&b_{2}&b_{3}\end{vmatrix}$
		$\displaystyle=\vec{\imath}\begin{vmatrix}a_{2}&a_{3}\\ b_{2}&b_{3}\end{vmatrix}-\vec{\jmath}\begin{vmatrix}a_{1}&a_{3}\\ b_{1}&b_{3}\end{vmatrix}+\vec{k}\begin{vmatrix}a_{1}&a_{2}\\ b_{1}&b_{2}\end{vmatrix}$
		$\displaystyle=(a_{2}b_{3}-a_{3}b_{2})\vec{\imath}-(a_{1}b_{3}-a_{3}b_{1})\vec{% \jmath}+(a_{1}b_{2}-a_{2}b_{1})\vec{k}$

Another way to remember the $3\times 3$ determinant is to repeat the first two columns after the original three:

\begin{matrix}\vec{\imath}&\vec{\jmath}&\vec{k}&\vec{\imath}&\vec{\jmath}\\ 2&-1&4&2&-1\\ 3&2&5&3&2\end{matrix}

This gives three full “upper left to lower right” diagonals, and three full “upper right to lower left” diagonals, as shown. Compute the products along each diagonal, then add the products on the right and subtract the products on the left:

\vec{u}\times\vec{v}=\big{(}-5\vec{\imath}+12\vec{\jmath}+4\vec{k}\,\big{)}-% \big{(}-3\vec{k}+8\vec{\imath}+10\vec{\jmath}\,\big{)}=-13\vec{\imath}+2\vec{% \jmath}+7\vec{k}=\left\langle-13,2,7\right\rangle.

This is equivalent to evaluating the determinant

	$\displaystyle\begin{vmatrix}\vec{\imath}&\vec{\jmath}&\vec{k}\\ 2&-1&4\\ 3&2&5\end{vmatrix}$	$\displaystyle=\begin{vmatrix}-1&4\\ 2&5\end{vmatrix}\vec{\imath}-\begin{vmatrix}2&4\\ 3&5\end{vmatrix}\vec{\jmath}+\begin{vmatrix}2&-1\\ 3&2\end{vmatrix}\vec{k}$
		$\displaystyle=(-5-8)\vec{\imath}-(10-12)\vec{\jmath}+(4-(-3))\vec{k}=-13\vec{% \imath}+2\vec{\jmath}+7\vec{k}.$

We practice using this method.

Example 11.4.2 Computing a cross product

Let $\vec{u}=\left\langle 1,3,6\right\rangle$ and $\vec{v}=\left\langle-1,2,1\right\rangle$ . Compute both $\vec{u}\times\vec{v}$ and $\vec{v}\times\vec{u}$ .

SolutionTo compute $\vec{u}\times\vec{v}$ , we form the matrix as prescribed above, complete with repeated first columns:

\begin{array}[]{ccccc}\ \vec{\imath}&\ \vec{\jmath}&\ \vec{k}&\ \vec{\imath}&% \ \vec{\jmath}\\ 1&3&6&1&3\\ -1&2&1&-1&2\end{array}

We let the reader compute the products of the diagonals; we give the result:

\vec{u}\times\vec{v}=\big{(}3\vec{\imath}-6\vec{\jmath}+2\vec{k}\,\big{)}-\big% {(}-3\vec{k}+12\vec{\imath}+\vec{\jmath}\,\big{)}=\left\langle-9,-7,5\right\rangle.

To compute $\vec{v}\times\vec{u}$ , we switch the second and third rows of the above matrix, then multiply along diagonals and subtract:

\begin{array}[]{ccccc}\ \vec{\imath}&\ \vec{\jmath}&\ \vec{k}&\ \vec{\imath}&% \ \vec{\jmath}\\ -1&2&1&-1&2\\ 1&3&6&1&3\end{array}

Note how with the rows being switched, the products that once appeared on the right now appear on the left, and vice-versa. Thus the result is:

\vec{v}\times\vec{u}=\big{(}12\vec{\imath}+\vec{\jmath}-3\vec{k}\,\big{)}-\big% {(}2\vec{k}+3\vec{\imath}-6\vec{\jmath}\,\big{)}=\left\langle 9,7,-5\right\rangle,

which is the opposite of $\vec{u}\times\vec{v}$ . We leave it to the reader to verify that each of these vectors is orthogonal to $\vec{u}$ and $\vec{v}$ .

Properties of the Cross Product

It is not coincidence that $\vec{v}\times\vec{u}=-(\vec{u}\times\vec{v})$ in the preceding example; one can show using Definition 11.4.1 that this will always be the case. The following theorem states several useful properties of the cross product, each of which can be verified by referring to the definition.

Theorem 11.4.1 Properties of the Cross Product

Let $\vec{u}$ , $\vec{v}$ and $\vec{w}$ be vectors in $\mathbb{R}^{3}$ and let $c$ be a scalar. The following identities hold:

1.

$\vec{u}\times\vec{v}=-(\vec{v}\times\vec{u})$

Anticommutative Property
2.
1. (a)
  
  $(\vec{u}+\vec{v})\times\vec{w}=\vec{u}\times\vec{w}+\vec{v}\times\vec{w}$
  
  Distributive Properties
2. (b)
  
  $\vec{u}\times(\vec{v}+\vec{w})=\vec{u}\times\vec{v}+\vec{u}\times\vec{w}$
3.

$c(\vec{u}\times\vec{v})=(c\vec{u})\times\vec{v}=\vec{u}\times(c\vec{v})$
4.
1. (a)
  
  $(\vec{u}\times\vec{v})\cdot\vec{u}=0$
  
  Orthogonality Properties
2. (b)
  
  $(\vec{u}\times\vec{v})\cdot\vec{v}=0$
5.

$\vec{u}\times\vec{u}=\vec{0}$
6.

$\vec{u}\times\vec{0}=\vec{0}$
7.

$\vec{u}\cdot(\vec{v}\times\vec{w})=(\vec{u}\times\vec{v})\cdot\vec{w}$

Scalar Triple Product

We introduced the cross product as a way to find a vector orthogonal to two given vectors, but we did not give a proof that the construction given in Definition 11.4.1 satisfies this property. Theorem 11.4.1 asserts this property holds; we leave the verification to Exercise 47.

Property 5 from the theorem is also left to the reader to prove in Exercise 48, but it reveals something more interesting than “the cross product of a vector with itself is $\vec{0}$ .” Let $\vec{u}$ and $\vec{v}$ be parallel vectors; that is, let there be a scalar $c$ such that $\vec{v}=c\vec{u}$ . Consider their cross product:

$\displaystyle\vec{u}\times\vec{v}$	$\displaystyle=\vec{u}\times(c\vec{u})$
	$\displaystyle=c(\vec{u}\times\vec{u})$	(by Property 3 of Theorem 11.4.1)
	$\displaystyle=\vec{0}.$	(by Property 5 of Theorem 11.4.1)

We have just shown that the cross product of parallel vectors is $\vec{0}$ . This hints at something deeper. Theorem 11.3.2 related the angle between two vectors and their dot product; there is a similar relationship relating the cross product of two vectors and the angle between them, given by the following theorem.

Theorem 11.4.2 The Cross Product and Angles

Let $\vec{u}$ and $\vec{v}$ be vectors in $\mathbb{R}^{3}$ . Then

\left\lVert\vec{u}\times\vec{v}\right\rVert=\left\lVert\vec{u}\right\rVert\,% \left\lVert\vec{v}\right\rVert\sin\theta,

where $\theta$ , $0\leq\theta\leq\pi$ , is the angle between $\vec{u}$ and $\vec{v}$ .

^†^†margin: Note: Definition 11.3.2 (through Theorem 11.3.2) defines

\vec{u}

and

\vec{v}

to be orthogonal if

\vec{u}\cdot\vec{v}=0

. We could use Theorem 11.4.2 to define

\vec{u}

and

\vec{v}

are parallel if

\vec{u}\times\vec{v}=0

. By such a definition,

\vec{0}

would be both orthogonal and parallel to every vector. Apparent paradoxes such as this are not uncommon in mathematics and can be very useful. (See also the marginal note at Definition 11.2.5.)

Note that this theorem makes a statement about the magnitude of the cross product. When the angle between $\vec{u}$ and $\vec{v}$ is 0 or $\pi$ (i.e., the vectors are parallel), the magnitude of the cross product is 0. The only vector with a magnitude of 0 is $\vec{0}$ (see Property 9 of Theorem 11.2.1), hence the cross product of parallel vectors is $\vec{0}$ .

We demonstrate the truth of this theorem in the following example.

Example 11.4.3 The cross product and angles

Let $\vec{u}=\left\langle 1,3,6\right\rangle$ and $\vec{v}=\left\langle-1,2,1\right\rangle$ as in Example 11.4.2. Verify Theorem 11.4.2 by finding $\theta$ , the angle between $\vec{u}$ and $\vec{v}$ , and the magnitude of $\vec{u}\times\vec{v}$ .

SolutionWe use Theorem 11.3.2 to find the angle between $\vec{u}$ and $\vec{v}$ .

	$\displaystyle\theta$	$\displaystyle=\cos^{-1}\left(\frac{\vec{u}\cdot\vec{v}}{\left\lVert\vec{u}% \right\rVert\,\left\lVert\vec{v}\right\rVert}\right)$
		$\displaystyle=\cos^{-1}\left(\frac{11}{\sqrt{46}\sqrt{6}}\right)$
		$\displaystyle\approx 0.8471=48.54^{\circ}.$

Our work in Example 11.4.2 showed that $\vec{u}\times\vec{v}=\left\langle-9,-7,5\right\rangle$ , hence $\left\lVert\vec{u}\times\vec{v}\right\rVert=\sqrt{155}.$ Is $\left\lVert\vec{u}\times\vec{v}\right\rVert=\left\lVert\vec{u}\right\rVert\,% \left\lVert\vec{v}\right\rVert\sin\theta$ ? Using numerical approximations, we find:

	$\displaystyle\left\lVert\vec{u}\times\vec{v}\right\rVert$	$\displaystyle=\sqrt{155}$	$\displaystyle\left\lVert\vec{u}\right\rVert\,\left\lVert\vec{v}\right\rVert\sin\theta$	$\displaystyle=\sqrt{46}\sqrt{6}\sin 0.8471$
		$\displaystyle\approx 12.45.$		$\displaystyle\approx 12.45.$

Numerically, they seem equal. Using a right triangle, one can show that

\sin\left(\cos^{-1}\left(\frac{11}{\sqrt{46}\sqrt{6}}\right)\right)=\frac{% \sqrt{155}}{\sqrt{46}\sqrt{6}},

which allows us to verify the theorem exactly.

Right Hand Rule

The anticommutative property of the cross product demonstrates that $\vec{u}\times\vec{v}$ and $\vec{v}\times\vec{u}$ differ only by a sign — these vectors have the same magnitude but point in the opposite direction. When seeking a vector perpendicular to $\vec{u}$ and $\vec{v}$ , we essentially have two directions to choose from, one in the direction of $\vec{u}\times\vec{v}$ and one in the direction of $\vec{v}\times\vec{u}$ . Does it matter which we choose? How can we tell which one we will get without graphing, etc.?

^†^†margin:

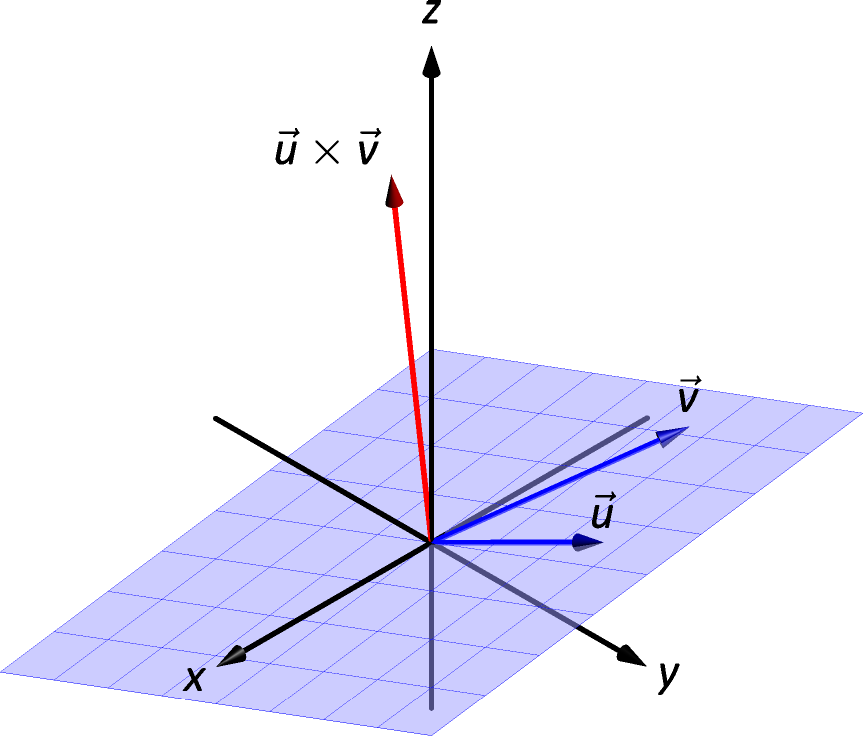Figure 11.4.1: Illustrating the Right Hand Rule of the cross product.

Another property of the cross product, as defined, is that it follows the right hand rule. Given $\vec{u}$ and $\vec{v}$ in $\mathbb{R}^{3}$ with the same initial point, point the index finger of your right hand in the direction of $\vec{u}$ and let your middle finger point in the direction of $\vec{v}$ (much as we did when establishing the right hand rule for the 3-dimensional coordinate system). Your thumb will naturally extend in the direction of $\vec{u}\times\vec{v}$ . One can “practice” this using Figure 11.4.1. If you switch, and point the index finder in the direction of $\vec{v}$ and the middle finger in the direction of $\vec{u}$ , your thumb will now point in the opposite direction, allowing you to “visualize” the anticommutative property of the cross product. In fact, we can use this property to define the cross product, which we summarize in the next key idea.

Key Idea 11.4.1 Alternate Definition of the Cross Product

For vectors $\vec{u}$ and $\vec{v}$ , the cross product $\vec{u}\times\vec{v}$ is the unique vector such that

1.

$\left\lVert\vec{u}\times\vec{v}\right\rVert=\left\lVert\vec{u}\right\rVert% \left\lVert\vec{v}\right\rVert\sin\theta$ where $\theta$ is the angle between $\vec{u}$ and $\vec{v}$ ,
2.

$\vec{u}\times\vec{v}$ is orthogonal to both $\vec{u}$ and $\vec{v}$ , and
3.

$\vec{u}$ , $\vec{v}$ , and $\vec{u}\times\vec{v}$ form a right-handed triple.

Applications of the Cross Product

There are a number of ways in which the cross product is useful in mathematics, physics and other areas of science beyond “just” finding a vector perpendicular to two others. We highlight a few here.

Area of a Parallelogram

^†^†margin: (a) (b) Figure 11.4.2: Using the cross product to find the area of a parallelogram.

It is a standard geometry fact that the area of a parallelogram is $A=bh$ , where $b$ is the length of the base and $h$ is the height of the parallelogram, as illustrated in Figure 11.4.2(a). As shown when defining the Parallelogram Law of vector addition, two vectors $\vec{u}$ and $\vec{v}$ define a parallelogram when drawn from the same initial point, as illustrated in Figure 11.4.2(b). Trigonometry tells us that $h=\left\lVert\vec{u}\right\rVert\sin\theta$ , hence the area of the parallelogram is

A=\left\lVert\vec{u}\right\rVert\,\left\lVert\vec{v}\right\rVert\sin\theta=% \left\lVert\vec{u}\times\vec{v}\right\rVert,

(11.5)

where the second equality comes from Theorem 11.4.2. We illustrate using Equation (11.5) in the following example.

Example 11.4.4 Finding the area of a parallelogram

1.

Find the area of the parallelogram defined by the vectors $\vec{u}=\left\langle 2,1\right\rangle$ and $\vec{v}=\left\langle 1,3\right\rangle$ .
2.

Verify that the points $A=(1,1,1)$ , $B=(2,3,2)$ , $C=(4,5,3)$ and $D=(3,3,2)$ are the vertices of a parallelogram. Find the area of the parallelogram.

Solution

1.

Figure 11.4.3(a) sketches the parallelogram defined by the vectors $\vec{u}$ and $\vec{v}$ . We have a slight problem in that our vectors exist in $\mathbb{R}^{2}$ , not $\mathbb{R}^{3}$ , and the cross product is only defined on vectors in $\mathbb{R}^{3}$ . We skirt this issue by viewing $\vec{u}$ and $\vec{v}$ as vectors in the $x-y$ plane of $\mathbb{R}^{3}$ , and rewrite them as $\vec{u}=\left\langle 2,1,0\right\rangle$ and $\vec{v}=\left\langle 1,3,0\right\rangle$ . We can now compute the cross product. ^†^†margin: (a) 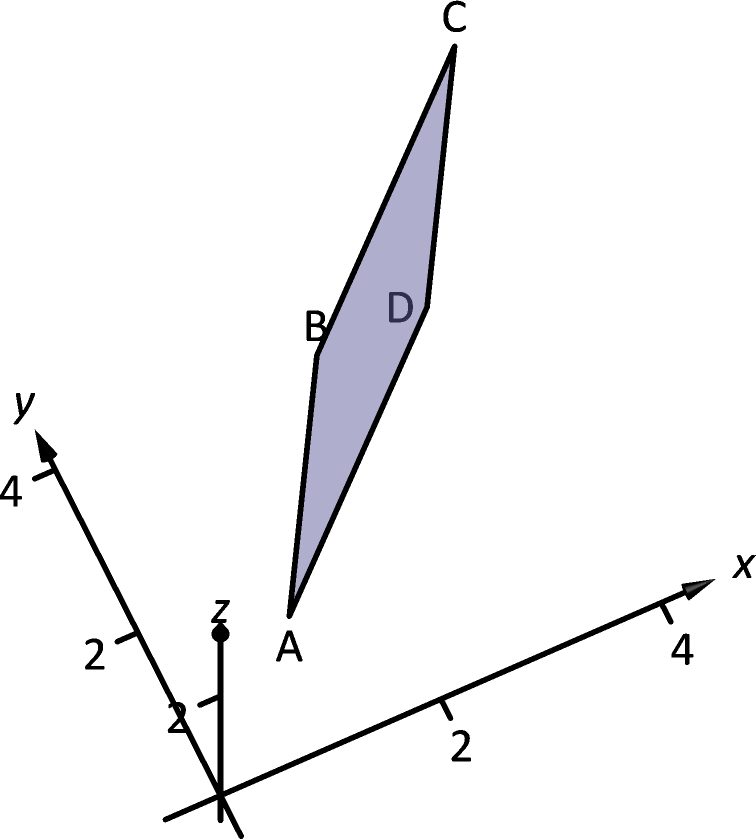(b) Figure 11.4.3: Sketching the parallelograms in Example 11.4.4. It is easy to show that $\vec{u}\times\vec{v}=\left\langle 0,0,5\right\rangle$ ; therefore the area of the parallelogram is $A=\left\lVert\vec{u}\times\vec{v}\right\rVert=5$ .
2.

To show that the quadrilateral $A B C D$ is a parallelogram (shown in Figure 11.4.3(b)), we need to show that the opposite sides are parallel. We can quickly show that $\vec{A}B=\vec{D}C=\left\langle 1,2,1\right\rangle$ and $\vec{B}C=\vec{A}D=\left\langle 2,2,1\right\rangle$ . We find the area by computing the magnitude of the cross product of $\vec{A}B$ and $\vec{B}C$ :

$\vec{A}B\times\vec{B}C=\left\langle 0,1,-2\right\rangle\quad\Rightarrow\quad% \left\lVert\vec{A}B\times\vec{B}C\right\rVert=\sqrt{5}.$

This application is more commonly used to find the area of a triangle (because triangles are used more often than parallelograms). We illustrate this in the following example.

Example 11.4.5 Area of a triangle

Find the area of the triangle with vertices $A=(1,2)$ , $B=(2,3)$ and $C=(3,1)$ , as pictured in Figure 11.4.4.

SolutionWe found the area of this triangle in Example 6.1.5 to be $1.5$ using integration. There we discussed the fact that finding the area of a triangle can be inconvenient using the “ $\frac{1}{2}bh$ ” formula as one has to compute the height, which generally involves finding angles, etc. Using a cross product is much more direct.

^†^†margin: Figure 11.4.4: Finding the area of a triangle in Example 11.4.5.

We can choose any two sides of the triangle to use to form vectors; we choose $\vec{A}B=\left\langle 1,1\right\rangle$ and $\vec{A}C=\left\langle 2,-1\right\rangle$ . As in the previous example, we will rewrite these vectors with a third component of 0 so that we can apply the cross product. The area of the triangle is

\frac{1}{2}\left\lVert\vec{A}B\times\vec{A}C\right\rVert=\frac{1}{2}\left% \lVert\left\langle 1,1,0\right\rangle\times\left\langle 2,-1,0\right\rangle% \right\rVert=\frac{1}{2}\left\lVert\left\langle 0,0,-3\right\rangle\right% \rVert=\frac{3}{2}.

We arrive at the same answer as before with less work.

Volume of a Parallelepiped

The three dimensional analogue to the parallelogram is the parallelepiped. Each face is parallel to the opposite face, as illustrated in Figure 11.4.5. By crossing $\vec{v}$ and $\vec{w}$ , one gets a vector whose magnitude is the area of the base. Dotting this vector with $\vec{u}$ computes the volume of parallelepiped! (Up to a sign; take the absolute value.)

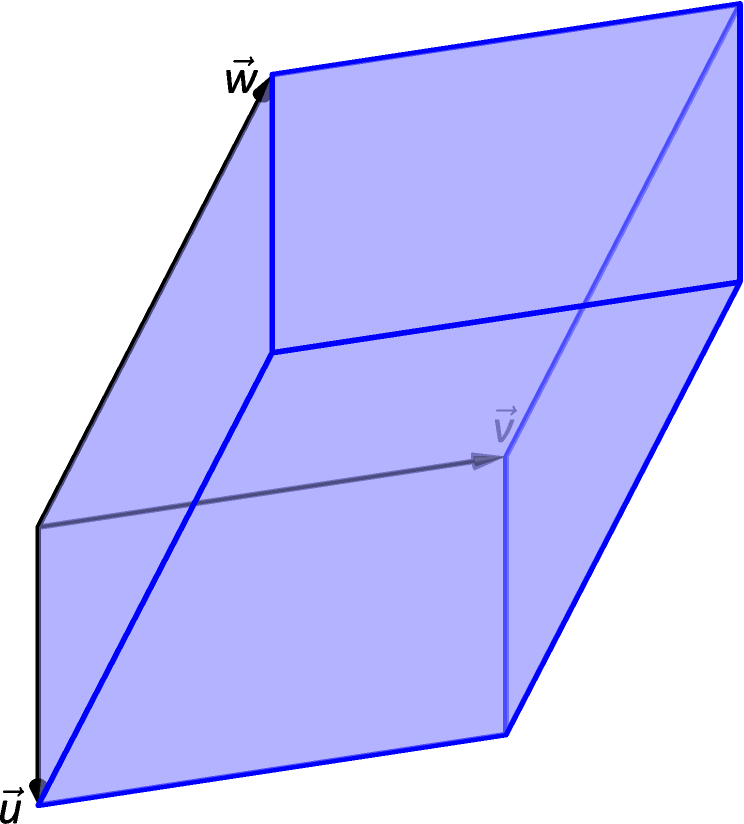^†^†margin: Note: The word “parallelepiped” is pronounced “parallel-eh-pipe-ed.” ^†^†margin:

Figure 11.4.5: A parallelepiped is the three dimensional analogue to the parallelogram.

Thus the volume of a parallelepiped defined by vectors $\vec{u}$ , $\vec{v}$ and $\vec{w}$ is

V=\left\lvert\vec{u}\cdot(\vec{v}\times\vec{w})\right\rvert.

(11.6)

Note how this is the Scalar Triple Product, first seen in Theorem 11.4.1. Applying the identities given in the theorem shows that we can apply the Scalar Triple Product in any “order” we choose to find the volume. That is,

V=\left\lvert\vec{u}\cdot(\vec{v}\times\vec{w})\right\rvert=\left\lvert\vec{u}% \cdot(\vec{w}\times\vec{v})\right\rvert=\left\lvert(\vec{u}\times\vec{v})\cdot% \vec{w}\right\rvert,\quad\text{etc.}

As with the cross product, we can also write $\vec{u}\cdot(\vec{v}\times\vec{w})$ in terms of a determinant:

\vec{u}\cdot(\vec{v}\times\vec{w})=\begin{vmatrix}u_{1}&u_{2}&u_{3}\\ v_{1}&v_{2}&v_{3}\\ w_{1}&w_{2}&w_{3}\end{vmatrix}.

Because the volume is the absolute value of the determinant, changing the order of the rows can only change the sign of this determinant, which doesn’t change the final answer.

^†^†margin:

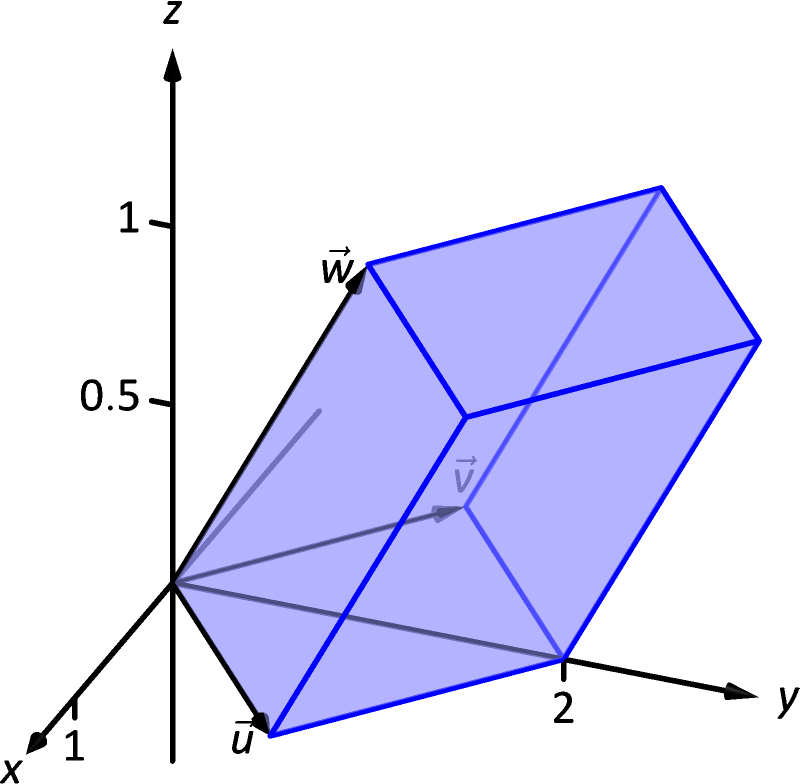Figure 11.4.6: A parallelepiped in Example 11.4.6.

Example 11.4.6 Finding the volume of parallelepiped

Find the volume of the parallelepiped defined by the vectors $\vec{u}=\left\langle 1,1,0\right\rangle$ , $\vec{v}=\left\langle-1,1,0\right\rangle$ and $\vec{w}=\left\langle 0,1,1\right\rangle$ .

SolutionWe apply Equation (11.6). We first find $\vec{v}\times\vec{w}=\left\langle 1,1,-1\right\rangle$ . Then

\left\lvert\vec{u}\cdot(\vec{v}\times\vec{w})\right\rvert=\left\lvert\left% \langle 1,1,0\right\rangle\cdot\left\langle 1,1,-1\right\rangle\right\rvert=2.

So the volume of the parallelepiped is 2 cubic units. In terms of determinants, we have

\begin{vmatrix}1&1&0\\ -1&1&0\\ 0&1&1\end{vmatrix}=\begin{vmatrix}1&0\\ 1&1\end{vmatrix}1-\begin{vmatrix}-1&0\\ 0&1\end{vmatrix}1+\begin{vmatrix}-1&1\\ 0&1\end{vmatrix}0(1-0)1-(-1-0)1=1+1=2,

and the absolute value of this determinant is again 2.

Torque

Torque is a measure of the turning force applied to an object. A classic scenario involving torque is the application of a wrench to a bolt. When a force is applied to the wrench, the bolt turns. When we represent the force and wrench with vectors $\vec{F}$ and $\vec{\ell}$ , we see that the bolt moves (because of the threads) in a direction orthogonal to $\vec{F}$ and $\vec{\ell}$ . Torque is usually represented by the Greek letter $\tau$ , or tau, and has units of N $\cdot$ m, a newton-meter, or ft $\cdot$ lb, a foot-pound.

While a full understanding of torque is beyond the purposes of this book, when a force $\vec{F}$ is applied to a lever arm $\vec{\ell}$ , the resulting torque is

\vec{\tau}=\vec{\ell}\times\vec{F}.

(11.7)

Example 11.4.7 Computing torque

A lever of length 2ft makes an angle with the horizontal of $45^{\circ}$ . Find the resulting torque when a force of 10lb is applied to the end of the level where:

^†^†margin: Figure 11.4.7: Showing a force being applied to a lever in Example 11.4.7.

1.

the force is perpendicular to the lever, and
2.

the force makes an angle of $60^{\circ}$ with the lever, as shown in Figure 11.4.7.

Solution

1.

We start by determining vectors for the force and lever arm. Since the lever arm makes a $45^{\circ}$ angle with the horizontal and is 2ft long, we can state that $\vec{\ell}=2\left\langle\cos 45^{\circ},\sin 45^{\circ}\right\rangle=\left% \langle\sqrt{2},\sqrt{2}\right\rangle.$

Since the force vector is perpendicular to the lever arm (as seen in the left hand side of Figure 11.4.7), we can conclude it is making an angle of $-45^{\circ}$ with the horizontal. As it has a magnitude of 10lb, we can state $\vec{F}=10\left\langle\cos(-45^{\circ}),\sin(-45^{\circ})\right\rangle=\left% \langle 5\sqrt{2},-5\sqrt{2}\right\rangle.$

Using Equation (11.7) to find the torque requires a cross product. We again let the third component of each vector be 0 and compute the cross product:

$\displaystyle\vec{\tau}$ $\displaystyle=\vec{\ell}\times\vec{F}$

$\displaystyle=\left\langle\sqrt{2},\sqrt{2},0\right\rangle\times\left\langle 5% \sqrt{2},-5\sqrt{2},0\right\rangle$

$\displaystyle=\left\langle 0,0,-20\right\rangle$

This clearly has a magnitude of 20 ft-lb.

We can view the force and lever arm vectors as lying “on the page”; our computation of $\vec{\tau}$ shows that the torque goes “into the page.” This follows the Right Hand Rule of the cross product, and it also matches well with the example of the wrench turning the bolt. Turning a bolt clockwise moves it in.
2.

Our lever arm can still be represented by $\vec{\ell}=\left\langle\sqrt{2},\sqrt{2}\right\rangle$ . As our force vector makes a $60^{\circ}$ angle with $\vec{\ell}$ , we can see (referencing the right hand side of the figure) that $\vec{F}$ makes a $-15^{\circ}$ angle with the horizontal. Thus

$\displaystyle\vec{F}=10\left\langle\cos-15^{\circ},\sin-15^{\circ}\right\rangle$ $\displaystyle=\left\langle\frac{5(1+\sqrt{3})}{\sqrt{2}},\frac{5(1-\sqrt{3})}{% \sqrt{2}}\right\rangle.$

We again make the third component 0 and take the cross product to find the torque:

$\displaystyle\vec{\tau}$ $\displaystyle=\vec{\ell}\times\vec{F}$

$\displaystyle=\left\langle\sqrt{2},\sqrt{2},0\right\rangle\times\left\langle% \frac{5(1+\sqrt{3})}{\sqrt{2}},\frac{5(1-\sqrt{3})}{\sqrt{2}},0\right\rangle$

$\displaystyle=\left\langle 0,0,-10\sqrt{3}\right\rangle.$

As one might expect, when the force and lever arm vectors are orthogonal, the magnitude of force is greater than when the vectors are not orthogonal.

While the cross product has a variety of applications (as noted in this chapter), its fundamental use is finding a vector perpendicular to two others. Knowing a vector is orthogonal to two others is of incredible importance, as it allows us to find the equations of lines and planes in a variety of contexts. The importance of the cross product, in some sense, relies on the importance of lines and planes, which see widespread use throughout engineering, physics and mathematics. We study lines and planes in the next two sections.

Exercises 11.4

Terms and Concepts

1.

The cross product of two vectors is a , not a scalar.
2.
One can visualize the direction of $\vec{u}\times\vec{v}$ using the .
3.

Give a synonym for “orthogonal.”
4.

T/F: A fundamental principle of the cross product is that $\vec{u}\times\vec{v}$ is orthogonal to $\vec{u}$ and $\vec{v}$ .
5.

is a measure of the turning force applied to an object.
6.

T/F: If $\vec{u}$ and $\vec{v}$ are parallel, then $\vec{u}\times\vec{v}=\vec{0}$ .

Problems

7.

State whether each expression is meaningful. If not, explain why. If so, state whether it is a vector or a scalar.
1. (a)
  
  $\vec{a}\cdot(\vec{b}\times\vec{c})$
2. (b)
  
  $\vec{a}\times(\vec{b}\times\vec{c})$
3. (c)
  
  $(\vec{a}\cdot\vec{b})\times(\vec{c}\cdot\vec{d})$
1. (d)
  
  $\vec{a}\times(\vec{b}\cdot\vec{c})$
2. (e)
  
  $(\vec{a}\times\vec{b})(\vec{c}\times\vec{d})$
3. (f)
  
  $(\vec{a}\times\vec{b})\cdot(\vec{c}\times\vec{d})$
8.
For any $\vec{u}$ and $\vec{v}$ in $\mathbb{R}^{3}$ we have $\left\lVert\vec{u}\right\rVert^{2}\left\lVert\vec{v}\right\rVert^{2}=(\vec{u}% \cdot\vec{v})^{2}+\left\lVert\vec{u}\times\vec{v}\right\rVert^{2}.$ (This can be verified directly by a somewhat messy algebraic computation.) Use this formula to show that $\left\lVert\vec{u}\times\vec{v}\right\rVert=\left\lVert\vec{u}\right\rVert% \left\lVert\vec{v}\right\rVert\sin\theta$ where $\theta$ is the angle between $\vec{u}$ and $\vec{v}$ .

In Exercises 9–12, calculate the determinant.

9.

$\begin{vmatrix}4&1\\ 2&5\end{vmatrix}$
10.

$\begin{vmatrix}-1&2\\ \frac{1}{2}&4\end{vmatrix}$
11.

$\begin{vmatrix}1&2&3\\ 4&5&6\\ 7&8&9\end{vmatrix}$
12.

$\begin{vmatrix}2&1&3\\ 4&-1&-5\\ 1&2&1\end{vmatrix}$

In Exercises 13–20, vectors $\vec{u}$ and $\vec{v}$ are given. Compute $\vec{u}\times\vec{v}$ and show this is orthogonal to both $\vec{u}$ and $\vec{v}$ .

13.

$\vec{u}=\left\langle 3,2,-2\right\rangle$ , $\vec{v}=\left\langle 0,1,5\right\rangle$
14.

$\vec{u}=\left\langle 5,-4,3\right\rangle$ , $\vec{v}=\left\langle 2,-5,1\right\rangle$
15.

$\vec{u}=\left\langle 4,-5,-5\right\rangle$ , $\vec{v}=\left\langle 3,3,4\right\rangle$
16.

$\vec{u}=\left\langle-4,7,-10\right\rangle$ , $\vec{v}=\left\langle 4,4,1\right\rangle$
17.

$\vec{u}=\left\langle 1,0,1\right\rangle$ , $\vec{v}=\left\langle 5,0,7\right\rangle$
18.

$\vec{u}=\left\langle 1,5,-4\right\rangle$ , $\vec{v}=\left\langle-2,-10,8\right\rangle$
19.

$\vec{u}=\vec{\imath}$ , $\vec{v}=\vec{\jmath}$
20.

$\vec{u}=\vec{\imath}$ , $\vec{v}=\vec{k}$
21.

Pick any vectors $\vec{u}$ , $\vec{v}$ and $\vec{w}$ in $\mathbb{R}^{3}$ and show that $\vec{u}\times(\vec{v}+\vec{w})=\vec{u}\times\vec{v}+\vec{u}\times\vec{w}$ .
22.

Pick any vectors $\vec{u}$ , $\vec{v}$ and $\vec{w}$ in $\mathbb{R}^{3}$ and show that $\vec{u}\cdot(\vec{v}\times\vec{w})=(\vec{u}\times\vec{v})\cdot\vec{w}$ .

In Exercises 23–26, the magnitudes of vectors $\vec{u}$ and $\vec{v}$ in $\mathbb{R}^{3}$ are given, along with the angle $\theta$ between them. Use this information to find the magnitude of $\vec{u}\times\vec{v}$ .

23.

$\left\lVert\vec{u}\right\rVert=2$ , $\left\lVert\vec{v}\right\rVert=5$ , $\theta=30^{\circ}$
24.

$\left\lVert\vec{u}\right\rVert=3$ , $\left\lVert\vec{v}\right\rVert=7$ , $\theta=\pi/2$
25.

$\left\lVert\vec{u}\right\rVert=3$ , $\left\lVert\vec{v}\right\rVert=4$ , $\theta=\pi$
26.

$\left\lVert\vec{u}\right\rVert=2$ , $\left\lVert\vec{v}\right\rVert=5$ , $\theta=5\pi/6$

In Exercises 27–30, find the area of the parallelogram defined by the given vectors.

27.

$\vec{u}=\left\langle 1,1,2\right\rangle$ , $\vec{v}=\left\langle 2,0,3\right\rangle$
28.

$\vec{u}=\left\langle-2,1,5\right\rangle$ , $\vec{v}=\left\langle-1,3,1\right\rangle$
29.

$\vec{u}=\left\langle 1,2\right\rangle$ , $\vec{v}=\left\langle 2,1\right\rangle$
30.

$\vec{u}=\left\langle 2,0\right\rangle$ , $\vec{v}=\left\langle 0,3\right\rangle$

In Exercises 31–34, find the area of the triangle with the given vertices.

31.

Vertices: $(0,0,0)$ , $(1,3,-1)$ and $(2,1,1)$ .
32.

Vertices: $(5,2,-1)$ , $(3,6,2)$ and $(1,0,4)$ .
33.

Vertices: $(1,1)$ , $(1,3)$ and $(2,2)$ .
34.

Vertices: $(3,1)$ , $(1,2)$ and $(4,3)$ .

In Exercises 35–36, find the area of the quadrilateral with the given vertices. (Hint: break the quadrilateral into 2 triangles.)

35.

Vertices: $(0,0)$ , $(1,2)$ , $(3,0)$ and $(4,3)$ .
36.

Vertices: $(0,0,0)$ , $(2,1,1)$ , $(-1,2,-8)$ and $(1,-1,5)$ .

In Exercises 37–38, find the volume of the parallelepiped defined by the given vectors.

37.

$\vec{u}=\left\langle 1,1,1\right\rangle$ , $\vec{v}=\left\langle 1,2,3\right\rangle$ , $\vec{w}=\left\langle 1,0,1\right\rangle$
38.

$\vec{u}=\left\langle-1,2,1\right\rangle$ , $\vec{v}=\left\langle 2,2,1\right\rangle$ , $\vec{w}=\left\langle 3,1,3\right\rangle$

In Exercises 39–42, find a unit vector orthogonal to both $\vec{u}$ and $\vec{v}$ .

39.

$\vec{u}=\left\langle 1,1,1\right\rangle$ , $\vec{v}=\left\langle 2,0,1\right\rangle$
40.

$\vec{u}=\left\langle 1,-2,1\right\rangle$ , $\vec{v}=\left\langle 3,2,1\right\rangle$
41.

$\vec{u}=\left\langle 5,0,2\right\rangle$ , $\vec{v}=\left\langle-3,0,7\right\rangle$
42.

$\vec{u}=\left\langle 1,-2,1\right\rangle$ , $\vec{v}=\left\langle-2,4,-2\right\rangle$
43.

A bicycle rider applies 150lb of force, straight down, onto a pedal that extends 7in horizontally from the crankshaft. Find the magnitude of the torque applied to the crankshaft.
44.

A bicycle rider applies 150lb of force, straight down, onto a pedal that extends 7in from the crankshaft, making a $30^{\circ}$ angle with the horizontal. Find the magnitude of the torque applied to the crankshaft.
45.

To turn a stubborn bolt, 80lb of force is applied to a 10in wrench. What is the maximum amount of torque that can be applied to the bolt?
46.

To turn a stubborn bolt, 80lb of force is applied to a 10in wrench in a confined space, where the direction of applied force makes a $10^{\circ}$ angle with the wrench. How much torque is subsequently applied to the wrench?
47.

Show, using the definition of the Cross Product, that $\vec{u}\cdot(\vec{u}\times\vec{v})=0$ ; that is, that $\vec{u}$ is orthogonal to the cross product of $\vec{u}$ and $\vec{v}$ .
48.

Show, using the definition of the Cross Product, that $\vec{u}\times\vec{u}=\vec{0}$ .
49.

Suppose $\vec{a}$ , $\vec{v}$ , and $\vec{w}$ are vectors in $\mathbb{R}^{3}$ with $\vec{a}\neq\vec{0}$ . Show that if both $\vec{a}\cdot\vec{v}=\vec{a}\cdot\vec{w}$ and $\vec{a}\times\vec{v}=\vec{a}\times\vec{w}$ then $\vec{v}=\vec{w}$ .
50.

Show that $\begin{vmatrix}a&b\\ c&d\end{vmatrix}=0$ if and only if $\left\langle a,b\right\rangle$ and $\left\langle c,d\right\rangle$ are parallel.
51.

Show that $\vec{v}\times\vec{w}=\vec{0}$ if and only if $\vec{v}$ and $\vec{w}$ are parallel in $\mathbb{R}^{3}$ .
52.

Show that $\begin{vmatrix}c&d\\ a&b\end{vmatrix}=-\begin{vmatrix}a&b\\ c&d\end{vmatrix}$ .
53.

Show that $\vec{w}\times\vec{v}=-(\vec{v}\times\vec{w})$ for any $\vec{v}$ and $\vec{w}$ in $\mathbb{R}^{3}$ .
54.

Show that for any real numbers $s$ and $t$ we have $\begin{vmatrix}sa&sb\\ tc&td\end{vmatrix}=st\begin{vmatrix}a&b\\ c&d\end{vmatrix}$ .
55.

Show that $c(\vec{v}\times\vec{w})=\vec{v}\times(c\vec{w})$ for any scalar $c$ and for any $\vec{v}$ and $\vec{w}$ in $\mathbb{R}^{3}$ .
56.

Show that $\begin{vmatrix}a&b\\ c+s&d+t\end{vmatrix}=\begin{vmatrix}a&b\\ c&d\end{vmatrix}+\begin{vmatrix}a&b\\ s&t\end{vmatrix}$ .
57.

Show that $\vec{u}\times(\vec{v}+\vec{w})=\vec{u}\times\vec{v}+\vec{u}\times\vec{w}$ for any $\vec{u}$ , $\vec{v}$ , and $\vec{w}$ in $\mathbb{R}^{3}$ .
58.
Let $\vec{u}=\left\langle u_{1},u_{2},u_{3}\right\rangle$ , $\vec{v}=\left\langle v_{1},v_{2},v_{3}\right\rangle$ , and $\vec{w}=\left\langle w_{1},w_{2},w_{3}\right\rangle$ . Show that $\vec{u}\cdot(\vec{v}\times\vec{w})=\begin{vmatrix}u_{1}&u_{2}&u_{3}\\ v_{1}&v_{2}&v_{3}\\ w_{1}&w_{2}&w_{3}\end{vmatrix}$
59.

We have seen that if we swap two rows of a $2\times 2$ determinant the determinant changes sign. This is true for $3\times 3$ determinants as well. Using this fact show that $\vec{u}\cdot(\vec{v}\times\vec{w})=(\vec{u}\times\vec{v})\cdot\vec{w}$ for any vectors $\vec{u}$ , $\vec{v}$ and $\vec{w}$ in $\mathbb{R}^{3}$ .
60.

We have seen that if two rows of a $2\times 2$ determinant are the same the determinant is zero. This is true for $3\times 3$ determinants as well. Using this fact show that $\vec{v}\times\vec{w}$ is orthogonal to both $\vec{v}$ and $\vec{w}$ for any vectors $\vec{v}$ and $\vec{w}$ in $\mathbb{R}^{3}$ .

	$\displaystyle\vec{\tau}$	$\displaystyle=\vec{\ell}\times\vec{F}$
		$\displaystyle=\left\langle\sqrt{2},\sqrt{2},0\right\rangle\times\left\langle 5% \sqrt{2},-5\sqrt{2},0\right\rangle$
		$\displaystyle=\left\langle 0,0,-20\right\rangle$

	$\displaystyle\vec{\tau}$	$\displaystyle=\vec{\ell}\times\vec{F}$
		$\displaystyle=\left\langle\sqrt{2},\sqrt{2},0\right\rangle\times\left\langle% \frac{5(1+\sqrt{3})}{\sqrt{2}},\frac{5(1-\sqrt{3})}{\sqrt{2}},0\right\rangle$
		$\displaystyle=\left\langle 0,0,-10\sqrt{3}\right\rangle.$