Solutions To Selected Problems Chapter 10 Chapter 12

Chapter 11

Exercises 11.1

1.

right hand
3.

curve (a parabola); surface (a cylinder)
5.

a hyperboloid of two sheets
7.

$\left\lVert\overline{AB}\right\rVert=\sqrt{6}$ ; $\left\lVert\overline{BC}\right\rVert=\sqrt{17}$ ; $\left\lVert\overline{AC}\right\rVert=\sqrt{11}$ . Yes, it is a right triangle as $\left\lVert\overline{AB}\right\rVert^{2}+\left\lVert\overline{AC}\right\rVert^% {2}=\left\lVert\overline{BC}\right\rVert^{2}$ .
9.
11.

$\left\lVert\overline{AB}\right\rVert=\sqrt{29}$ , $\left\lVert\overline{AC}\right\rVert=\sqrt{105}$ , $\left\lVert\overline{BC}\right\rVert=2\sqrt{61}$ . The points do not lie on a line.
13.

Center at $(4,-1,0)$ ; radius = 3
15.

closer to the surface
17.

Interior of a sphere with radius 1 centered at the origin.
19.

The first octant of space along with its adjacent quarter planes; all points $(x,y,z)$ where each of $x$ , $y$ and $z$ are positive or zero. (Analogous to the first quadrant in the plane.)
21.
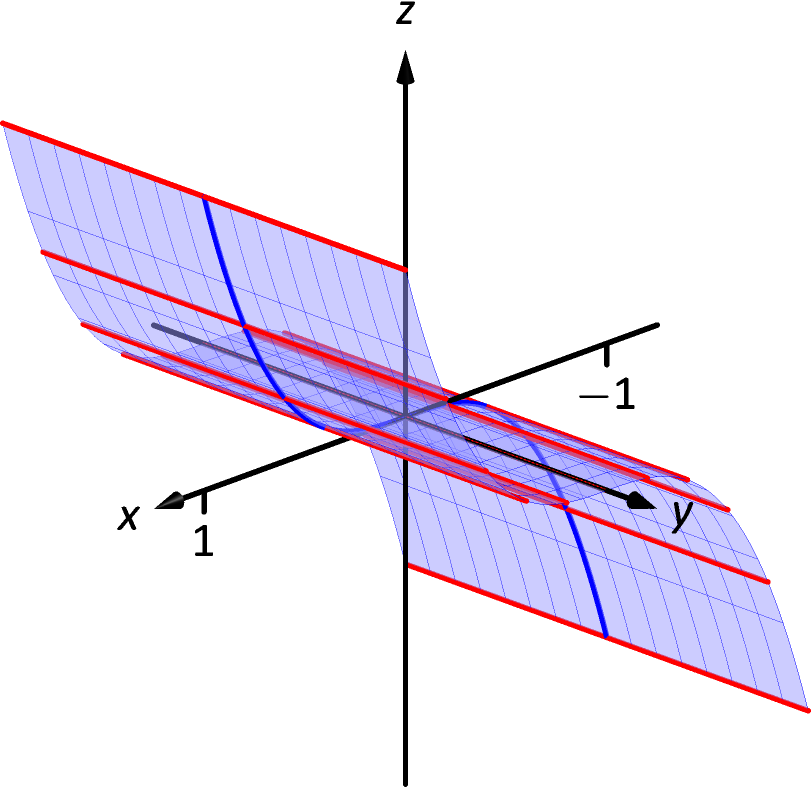
23.
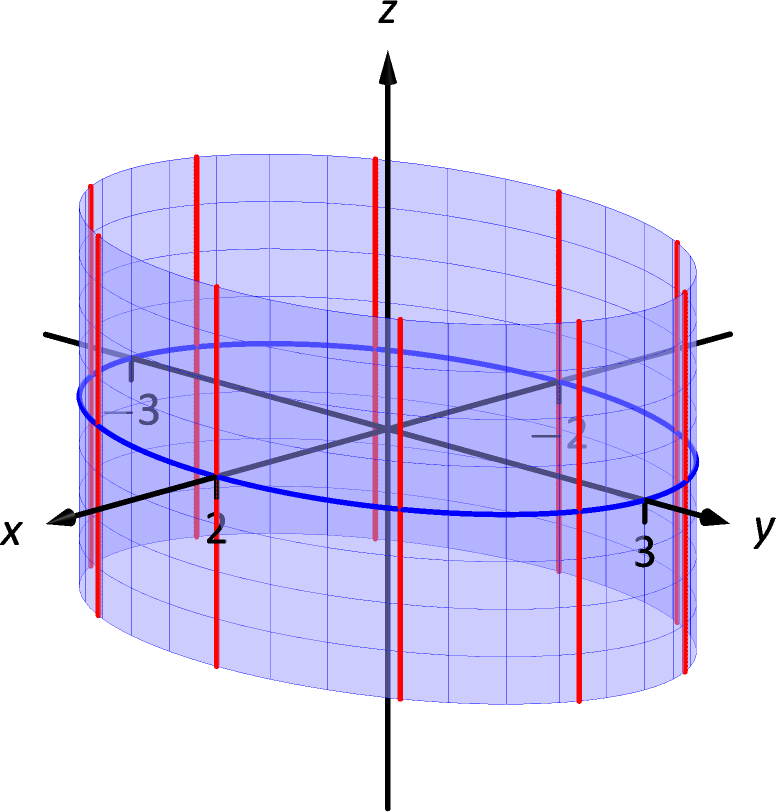
25.

$x^{2}+z^{2}=\frac{1}{(1+y^{2})^{2}}$
27.

$z=(\sqrt{x^{2}+y^{2}})^{2}=x^{2}+y^{2}$
29.

(a) $\displaystyle x=y^{2}+\frac{z^{2}}{9}$
31.

(b) $\displaystyle x^{2}+\frac{y^{2}}{9}+\frac{z^{2}}{4}=1$
33.
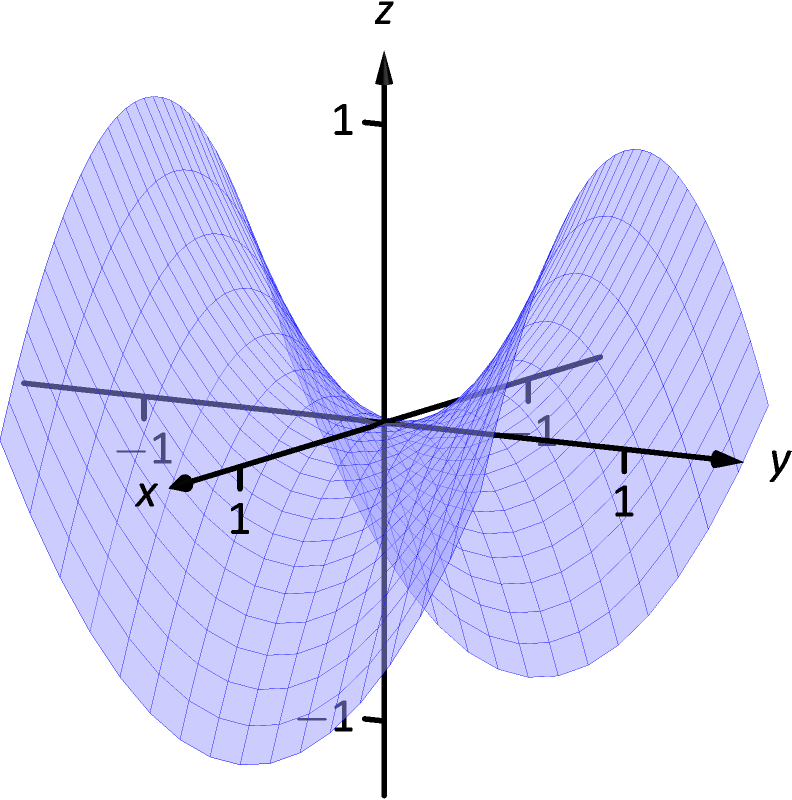
35.
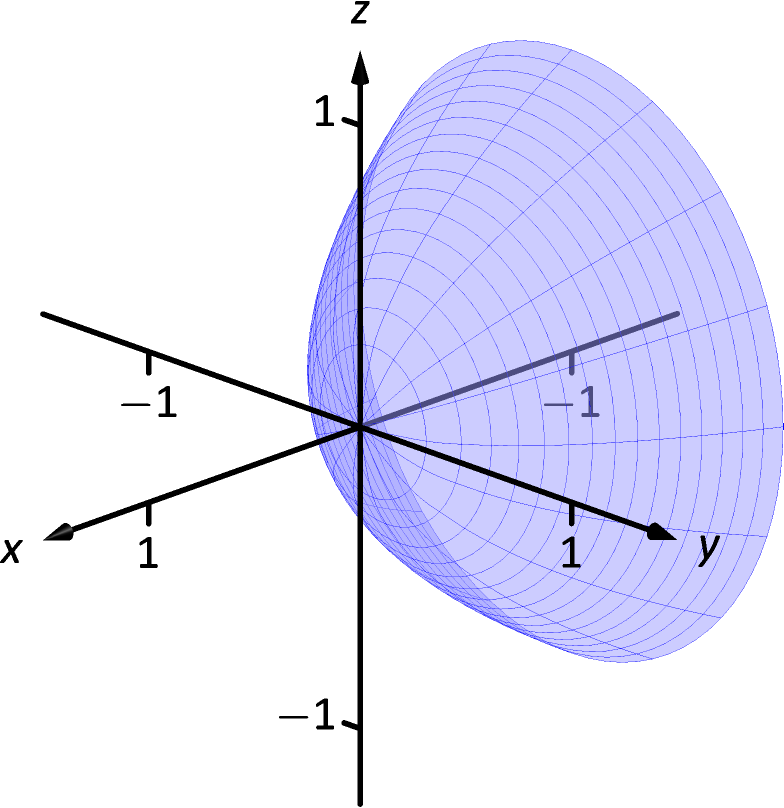
37.
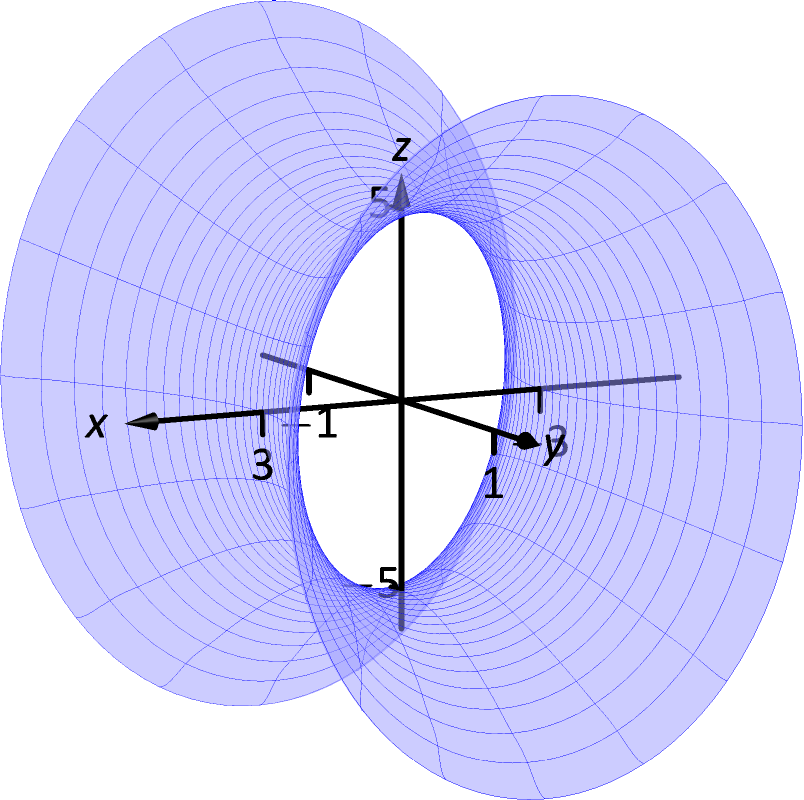
39.

Exercises 11.2

1.

Answers will vary.
3.

A vector with magnitude 1.
5.

Their respective unit vectors are parallel; unit vectors $\vec{u}_{1}$ and $\vec{u}_{2}$ are parallel if $\vec{u}_{1}=\pm\vec{u}_{2}$ .
7.

$\vec{P}Q=\left\langle 1,6\right\rangle=1\vec{\imath}+6\vec{\jmath}$
9.

$\vec{P}Q=\left\langle 6,-1,6\right\rangle=6\vec{\imath}-\vec{\jmath}+6\vec{k}$
11.
(a) $\vec{u}+\vec{v}=\left\langle 2,-1\right\rangle$ ; $\vec{u}-\vec{v}=\left\langle 0,-3\right\rangle$ ; $2\vec{u}-3\vec{v}=\left\langle-1,-7\right\rangle$ . (c) $\vec{x}=\left\langle 1/2,2\right\rangle$ .
13.
15.
17.

$\left\lVert\vec{u}\right\rVert=\sqrt{5}$ , $\left\lVert\vec{v}\right\rVert=\sqrt{13}$ , $\left\lVert\vec{u}+\vec{v}\right\rVert=\sqrt{26}$ , $\left\lVert\vec{u}-\vec{v}\right\rVert=\sqrt{10}$
19.

$\left\lVert\vec{u}\right\rVert=\sqrt{5}$ , $\left\lVert\vec{v}\right\rVert=3\sqrt{5}$ , $\left\lVert\vec{u}+\vec{v}\right\rVert=2\sqrt{5}$ , $\left\lVert\vec{u}-\vec{v}\right\rVert=4\sqrt{5}$
21.

$\vec{u}=\left\langle 3/\sqrt{58},7/\sqrt{58}\right\rangle$
23.

$\vec{u}=\left\langle 1/3,-2/3,2/3\right\rangle$
25.

When $\vec{u}$ and $\vec{v}$ have the same direction. (Note: parallel is not enough.)
27.

$\vec{u}=\left\langle\cos 120^{\circ},\sin 120^{\circ}\right\rangle=\left% \langle-1/2,\sqrt{3}/2\right\rangle$ .
29.

The magnitude of the force on each chain is $100/\sqrt{3}\approx 57.735$ lb.
31.

The magnitude of the force on the chain with angle $\theta$ is approx. $45.124$ lb; the magnitude of the force on the chain with angle $\varphi$ is approx. $59.629$ lb.
33.

$\theta=45^{\circ}$ ; the weight is lifted $0.29$ ft (about 3.5in).
35.

$\theta=45^{\circ}$ ; the weight is lifted $2.93$ ft.
37.
39.

Exercises 11.3

1.

Scalar
3.

By considering the sign of the dot product of the two vectors. If the dot product is positive, the angle is acute; if the dot product is negative, the angle is obtuse.
5.

$-22$
7.

$3$
9.

not defined
11.

Answers will vary.
13.

$\theta=0.3218\approx 18.43^{\circ}$
15.

$\theta=\pi/4=45^{\circ}$
17.

Answers will vary; two possible answers are $\left\langle-7,4\right\rangle$ and $\left\langle 14,-8\right\rangle$ .
19.

Answers will vary; two possible answers are $\left\langle 1,0,-1\right\rangle$ and $\left\langle 4,5,-9\right\rangle$ .
21.

$\text{proj}_{\,\vec{v}}{\,\vec{u}}=\left\langle-1/2,3/2\right\rangle$ .
23.

$\text{proj}_{\,\vec{v}}{\,\vec{u}}=\left\langle-1/2,-1/2\right\rangle$ .
25.

$\text{proj}_{\,\vec{v}}{\,\vec{u}}=\left\langle 1,2,3\right\rangle$ .
27.

$\vec{u}=\left\langle-1/2,3/2\right\rangle+\left\langle 3/2,1/2\right\rangle$ .
29.

$\vec{u}=\left\langle-1/2,-1/2\right\rangle+\left\langle-5/2,5/2\right\rangle$ .
31.

$\vec{u}=\left\langle 1,2,3\right\rangle+\left\langle 0,3,-2\right\rangle$ .
33.

1.96lb
35.

$141.42$ ft-lb
37.

$500$ ft-lb
39.

$500$ ft-lb
41.
43.
45.

Exercises 11.4

1.

vector
3.

“Perpendicular” is one answer.
5.

Torque
7.
(a) $\vec{a}\cdot(\vec{b}\times\vec{c})=\vec{a}\cdot(\text{vector})=\text{scalar}$ (b) $\vec{a}\times(\vec{b}\times\vec{c})=\vec{a}\times(\text{vector})=\text{vector}$ (c) $(\vec{a}\cdot\vec{b})\times(\vec{c}\cdot\vec{d})=(\text{scalar})\times(\text{% scalar})=\text{not meaningful}$ (d) $\vec{a}\times(\vec{b}\cdot\vec{c})=\vec{a}\cdot(\text{scalar})=\text{not meaningful}$ (e) $(\vec{a}\times\vec{b})(\vec{c}\times\vec{d})=(\text{vector})(\text{vector})=% \text{not meaningful}$ (f) $(\vec{a}\times\vec{b})\cdot(\vec{c}\times\vec{d})=(\text{vector})\cdot(\text{% vector})=\text{scalar}$
9.

18
11.

0
13.

$\vec{u}\times\vec{v}=\left\langle 12,-15,3\right\rangle$
15.

$\vec{u}\times\vec{v}=\left\langle-5,-31,27\right\rangle$
17.

$\vec{u}\times\vec{v}=\left\langle 0,-2,0\right\rangle$
19.

$\vec{\imath}\times\vec{\jmath}=\vec{k}$
21.

Answers will vary.
23.

5
25.

0
27.

$\sqrt{14}$
29.

$3$
31.

$5\sqrt{2}/2$
33.

$1$
35.

$7$
37.

$2$
39.

$\pm\frac{1}{\sqrt{6}}\left\langle 1,1,-2\right\rangle$
41.

$\left\langle 0,\pm 1,0\right\rangle$
43.

$87.5$ ft-lb
45.

$200/3\approx 66.67$ ft-lb
47.
With $\vec{u}=\left\langle u_{1},u_{2},u_{3}\right\rangle$ and $\vec{v}=\left\langle v_{1},v_{2},v_{3}\right\rangle$ , we have $\displaystyle\vec{u}\cdot(\vec{u}\times\vec{v})$ $\displaystyle=\left\langle u_{1},u_{2},u_{3}\right\rangle\cdot$ $\displaystyle\qquad(\left\langle u_{2}v_{3}-u_{3}v_{2},-(u_{1}v_{3}-u_{3}v_{1}% ),u_{1}v_{2}-u_{2}v_{1}\right\rangle)$ $\displaystyle=u_{1}(u_{2}v_{3}-u_{3}v_{2})-u_{2}(u_{1}v_{3}-u_{3}v_{1})$ $\displaystyle\qquad\qquad{}+u_{3}(u_{1}v_{2}-u_{2}v_{1})$ $\displaystyle=0.$
49.
51.
53.
55.
57.
59.

Exercises 11.5

1.

A point on the line and the direction of the line.
3.

parallel, skew
5.
vector: $\ell(t)=\left\langle 2,-4,1\right\rangle+t\left\langle 9,2,5\right\rangle$ parametric: $x=2+9t$ , $y=-4+2t$ , $z=1+5t$ symmetric: $(x-2)/9=(y+4)/2=(z-1)/5$
7.
Answers can vary: vector: $\ell(t)=\left\langle 2,1,5\right\rangle+t\left\langle 5,-3,-1\right\rangle$ parametric: $x=2+5t$ , $y=1-3t$ , $z=5-t$ symmetric: $(x-2)/5=-(y-1)/3=-(z-5)$
9.
Answers can vary; here the direction is given by $\vec{d}_{1}\times\vec{d}_{2}$ : vector: $\ell(t)=\left\langle 0,1,2\right\rangle+t\left\langle-10,43,9\right\rangle$ parametric: $x=-10t$ , $y=1+43t$ , $z=2+9t$ symmetric: $-x/10=(y-1)/43=(z-2)/9$
11.
Answers can vary; here the direction is given by $\vec{d}_{1}\times\vec{d}_{2}$ : vector: $\ell(t)=\left\langle 7,2,-1\right\rangle+t\left\langle 1,-1,2\right\rangle$ parametric: $x=7+t$ , $y=2-t$ , $z=-1+2t$ symmetric: $x-7=2-y=(z+1)/2$
13.
vector: $\ell(t)=\left\langle 1,1\right\rangle+t\left\langle 2,3\right\rangle$ parametric: $x=1+2t$ , $y=1+3t$ symmetric: $(x-1)/2=(y-1)/3$
15.

parallel
17.

intersecting; $\vec{\ell}_{1}(3)=\vec{\ell}_{2}(4)=\left\langle 9,-5,13\right\rangle$
19.

skew
21.

same
23.

$\sqrt{41}/3$
25.

$5\sqrt{2}/2$
27.

$3/\sqrt{2}$
29.

Since both $P$ and $Q$ are on the line, $\vec{P}Q$ is parallel to $\vec{d}$ . Thus $\vec{P}Q\times\vec{d}=\vec{0}$ , giving a distance of $0$ .
31.
(a) The distance formula cannot be used because since $\vec{d}_{1}$ and $\vec{d}_{2}$ are parallel, $\vec{c}$ is $\vec{0}$ and we cannot divide by $\left\lVert\vec{0}\right\rVert$ . (b) Since $\vec{d}_{1}$ and $\vec{d}_{2}$ are parallel, $\vec{P}_{1}P_{2}$ lies in the plane formed by the two lines. Thus $\vec{P}_{1}P_{2}\times\vec{d}_{2}$ is orthogonal to this plane, and $\vec{c}=(\vec{P}_{1}P_{2}\times\vec{d}_{2})\times\vec{d}_{2}$ is parallel to the plane, but still orthogonal to both $\vec{d}_{1}$ and $\vec{d}_{2}$ . We desire the length of the projection of $\vec{P}_{1}P_{2}$ onto $\vec{c}$ , which is what the formula provides. (c) Since the lines are parallel, one can measure the distance between the lines at any location on either line (just as to find the distance between straight railroad tracks, one can use a measuring tape anywhere along the track, not just at one specific place.) Let $P=P_{1}$ and $Q=P_{2}$ as given by the equations of the lines, and apply the formula for distance between a point and a line.

Exercises 11.6

1.

A point in the plane and a normal vector (i.e., a direction orthogonal to the plane).
3.

Answers will vary.
5.

Answers will vary.
7.
Standard form: $3(x-2)-(y-3)+7(z-4)=0$ general form: $3x-y+7z=31$
9.
Answers may vary; Standard form: $8(x-1)+4(y-2)-4(z-3)=0$ general form: $8x+4y-4z=4$
11.
Answers may vary; Standard form: $-7(x-2)+2(y-1)+(z-2)=0$ general form: $-7x+2y+z=-10$
13.
Answers may vary; Standard form: $2(x-1)-(y-1)=0$ general form: $2x-y=1$
15.
Answers may vary; Standard form: $2(x-2)-(y+6)-4(z-1)=0$ general form: $2x-y-4z=6$
17.
Answers may vary; Standard form: $(x-5)+(y-7)+(z-3)=0$ general form: $x+y+z=15$
19.
Answers may vary; Standard form: $3(x+4)+8(y-7)-10(z-2)=0$ general form: $3x+8y-10z=24$
21.
Answers may vary: $\ell=\left\{\begin{aligned} \displaystyle x&\displaystyle=14t\\ \displaystyle y&\displaystyle=-1-10t\\ \displaystyle z&\displaystyle=2-8t\end{aligned}\right.$
23.

$(-3,-7,-5)$
25.

No point of intersection; the plane and line are parallel.
27.

$\sqrt{5/7}$
29.

$1/\sqrt{3}$
31.

If $P$ is any point in the plane, and $Q$ is also in the plane, then $\vec{P}Q$ lies parallel to the plane and is orthogonal to $\vec{n}$ , the normal vector. Thus $\vec{n}\cdot\vec{P}Q=0$ , giving the distance as 0.