Solutions To Selected Problems Chapter 11 Chapter 13

Chapter 12

Exercises 12.1

1.

parametric equations
3.

displacement
5.
7.
9.
11.
13.
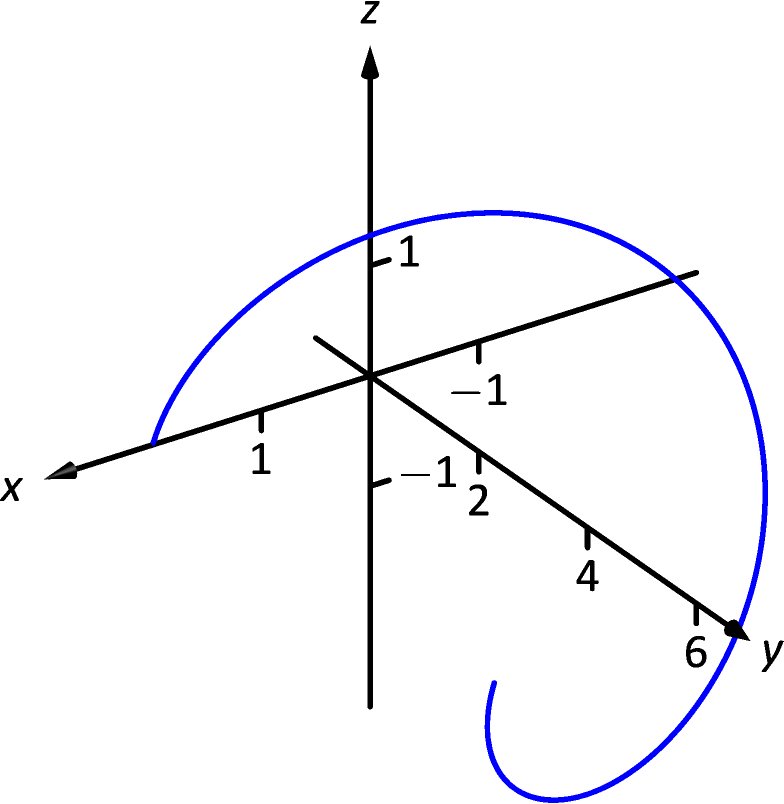
15.
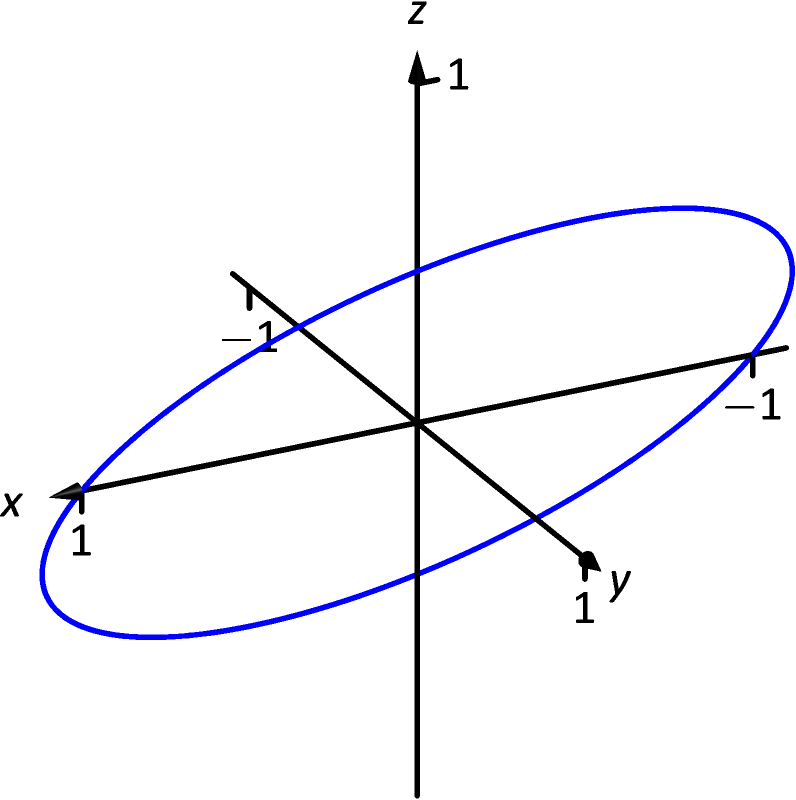
17.

$\left\lVert\vec{r}(t)\right\rVert=\sqrt{t^{2}+t^{4}}=\left\lvert t\right\rvert% \sqrt{t^{2}+1}$ .
19.

$\left\lVert\vec{r}(t)\right\rVert=\sqrt{4\cos^{2}t+4\sin^{2}t+t^{2}}=\sqrt{t^{% 2}+4}$ .
21.
Answers may vary, though most direct solution is $\vec{r}(t)=\left\langle 2\cos t+1,2\sin t+2\right\rangle$ .
23.
Answers may vary, though most direct solution is $\vec{r}(t)=\left\langle 1.5\cos t,5\sin t\right\rangle$ .
25.
Answers may vary, though most direct solutions are $\vec{r}(t)=\left\langle t,5(t-2)+3\right\rangle$ and $\vec{r}(t)=\left\langle t+2,5t+3\right\rangle$ .
27.
Answers may vary, though most direct solution is $\vec{r}(t)=\left\langle 2\cos t,2\sin t,2t\right\rangle$ .
29.

Answers may vary, though most direct solution is $\vec{r}(t)=\left\langle R\cos(2\pi Nt),R\sin(2\pi Nt),h\right\rangle$ .
31.

$\left\langle 1,0\right\rangle$
33.

$\left\langle 0,0,1\right\rangle$

Exercises 12.2

1.

component
3.

It is difficult to identify the points on the graphs of $\vec{r}(t)$ and $\vec{r}\hskip 1.25pt^{\prime}(t)$ that correspond to each other.
5.

$\left\langle 11,74,\sin 5\right\rangle$
7.

$\left\langle 1,e\right\rangle$
9.

$(-\infty,0)\bigcup(0,\infty)$
11.

$\vec{r}\hskip 1.25pt^{\prime}(t)=\left\langle-\sin t,e^{t},1/t\right\rangle$
13.

$\vec{r}\hskip 1.25pt^{\prime}(t)=(2t)\left\langle\sin t,2t+5\right\rangle+(t^{% 2})\left\langle\cos t,2\right\rangle=\left\langle 2t\sin t+t^{2}\cos t,6t^{2}+% 10t\right\rangle$
15.
$\vec{r}\hskip 1.25pt^{\prime}(t)=\left\langle 2t,1,0\right\rangle\times\left% \langle\sin t,2t+5,1\right\rangle+\left\langle t^{2}+1,t-1,1\right\rangle% \times\left\langle\cos t,2,0\right\rangle=$ $\left\langle-1,\cos t-2t,6t^{2}+10t+2+\cos t-\sin t-t\cos t\right\rangle$
17.
$\vec{r}\hskip 1.25pt^{\prime}(t)=\left\langle 2t+1,2t-1\right\rangle$
19.
$\vec{r}\hskip 1.25pt^{\prime}(t)=\left\langle 2t,3t^{2}-1\right\rangle$
21.

$\ell(t)=\left\langle 2,0\right\rangle+t\left\langle 3,1\right\rangle$
23.

$\ell(t)=\left\langle-3,0,\pi\right\rangle+t\left\langle 0,-3,1\right\rangle$
25.
$t=2n\pi$ , where $n$ is an integer; so $t=\dotsc-4\pi,-2\pi,0,2\pi,4\pi,\dotsc$
27.

$\vec{r}(t)$ is not smooth at $t=3\pi/4+n\pi$ , where $n$ is an integer
29.

Both derivatives return $\left\langle 5t^{4},4t^{3}-3t^{2},3t^{2}\right\rangle$ .
31.
Both derivatives return $\left\langle 2t-e^{t}-1,\cos t-3t^{2},(t^{2}+2t)e^{t}-(t-1)\cos t-\sin t\right\rangle$ .
33.

$\left\langle\frac{1}{4}t^{4},\sin t,te^{t}-e^{t}\right\rangle+\vec{C}$
35.

$\left\langle-2,0\right\rangle$
37.

$\vec{r}(t)=\left\langle\frac{1}{2}t^{2}+2,-\cos t+3\right\rangle$
39.

$\vec{r}(t)=\left\langle t^{4}/12+t+4,\ t^{3}/6+2t+5,\ t^{2}/2+3t+6\right\rangle$
41.

$2\sqrt{13}\pi$
43.

$\frac{1}{54}\left((22)^{3/2}-8\right)$
45.

12
47.
As $\vec{r}(t)$ has constant length, $\vec{r}(t)\cdot\vec{r}(t)=c^{2}$ for some constant $c$ . Thus $\displaystyle\vec{r}(t)\cdot\vec{r}(t)$ $\displaystyle=c^{2}$ $\displaystyle\frac{d}{dt}\big{(}\vec{r}(t)\cdot\vec{r}(t)\big{)}$ $\displaystyle=\frac{d}{dt}\big{(}c^{2}\big{)}$ $\displaystyle\vec{r}\hskip 1.25pt^{\prime}(t)\cdot\vec{r}(t)+\vec{r}(t)\cdot% \vec{r}\hskip 1.25pt^{\prime}(t)$ $\displaystyle=0$ $\displaystyle 2\vec{r}(t)\cdot\vec{r}\hskip 1.25pt^{\prime}(t)$ $\displaystyle=0$ $\displaystyle\vec{r}(t)\cdot\vec{r}\hskip 1.25pt^{\prime}(t)$ $\displaystyle=0.$

Exercises 12.3

1.

Velocity is a vector, indicating an objects direction of travel and its rate of distance change (i.e., its speed). Speed is a scalar.
3.

The average velocity is found by dividing the displacement by the time traveled — it is a vector. The average speed is found by dividing the distance traveled by the time traveled — it is a scalar.
5.

One example is traveling at a constant speed $s$ in a circle, ending at the starting position. Since the displacement is $\vec{0}$ , the average velocity is $\vec{0}$ , hence $\left\lVert\vec{0}\right\rVert=0$ . But traveling at constant speed $s$ means the average speed is also $s>0$ .
7.

$\vec{v}(t)=\left\langle 2,5,0\right\rangle$ , $\vec{a}(t)=\left\langle 0,0,0\right\rangle$
9.

$\vec{v}(t)=\left\langle-\sin t,\cos t\right\rangle$ , $\vec{a}(t)=\left\langle-\cos t,-\sin t\right\rangle$
11.

$\vec{v}(t)=\left\langle 1,\cos t\right\rangle$ , $\vec{a}(t)=\left\langle 0,-\sin t\right\rangle$
13.

$\vec{v}(t)=\left\langle 2t+1,-2t+2\right\rangle$ , $\vec{a}(t)=\left\langle 2,-2\right\rangle$
15.
$\left\lVert\vec{v}(t)\right\rVert=\sqrt{4t^{2}+1}$ . Min at $t=0$ ; Max at $t=\pm 1$ .
17.
$\left\lVert\vec{v}(t)\right\rVert=5$ . Speed is constant, so there is no difference between min/max
19.
$\left\lVert\vec{v}(t)\right\rVert=\left\lvert\sec t\right\rvert\sqrt{\tan^{2}t% +\sec^{2}t}$ . min: $t=0$ ; max: $t=\pi/4$
21.
$\left\lVert\vec{v}(t)\right\rVert=13$ . speed is constant, so there is no difference between min/max
23.
$\left\lVert\vec{v}(t)\right\rVert=\sqrt{4t^{2}+1+t^{2}/(1-t^{2})}$ . min: $t=0$ ; max: there is no max; speed approaches $\infty$ as $t\to\pm 1$
25.
(a) $\vec{r}_{1}(1)=\left\langle 1,1\right\rangle$ ; $\vec{r}_{2}(1)=\left\langle 1,1\right\rangle$ (b) $\vec{v}_{1}(1)=\left\langle 1,2\right\rangle$ ; $\left\lVert\vec{v}_{1}(1)\right\rVert=\sqrt{5}$ ; $\vec{a}_{1}(1)=\left\langle 0,2\right\rangle$ $\vec{v}_{2}(1)=\left\langle 2,4\right\rangle$ ; $\left\lVert\vec{v}_{2}(1)\right\rVert=2\sqrt{5}$ ; $\vec{a}_{2}(1)=\left\langle 2,12\right\rangle$
27.
(a) $\vec{r}_{1}(2)=\left\langle 6,4\right\rangle$ ; $\vec{r}_{2}(2)=\left\langle 6,4\right\rangle$ (b) $\vec{v}_{1}(2)=\left\langle 3,2\right\rangle$ ; $\left\lVert\vec{v}_{1}(2)\right\rVert=\sqrt{13}$ ; $\vec{a}_{1}(2)=\left\langle 0,0\right\rangle$ $\vec{v}_{2}(2)=\left\langle 6,4\right\rangle$ ; $\left\lVert\vec{v}_{2}(2)\right\rVert=2\sqrt{13}$ ; $\vec{a}_{2}(2)=\left\langle 0,0\right\rangle$
29.
$\vec{v}(t)=\left\langle 2t+1,3t+2\right\rangle$ , $\vec{r}(t)=\left\langle t^{2}+t+5,3t^{2}/2+2t-2\right\rangle$
31.

$\vec{v}(t)=\left\langle\sin t,\cos t\right\rangle$ , $\vec{r}(t)=\left\langle 1-\cos t,\sin t\right\rangle$
33.

Displacement: $\left\langle 0,0,6\pi\right\rangle$ ; distance traveled: $2\sqrt{13}\pi\approx 22.65$ ft; average velocity: $\left\langle 0,0,3\right\rangle$ ; average speed: $\sqrt{13}\approx 3.61$ ft/s
35.

Displacement: $\left\langle 0,0\right\rangle$ ; distance traveled: $2\pi\approx 6.28$ ft; average velocity: $\left\langle 0,0\right\rangle$ ; average speed: $1$ ft/s
37.

At $t$ -values of $\sin^{-1}(9/30)/(4\pi)+n/2\approx 0.024+n/2$ seconds, where $n$ is an integer.
39.
(a) Holding the crossbow at an angle of $0.013$ radians, $\approx 0.745^{\circ}$ will hit the target $0.4$ s later. (Another solution exists, with an angle of $89^{\circ}$ , landing $18.75$ s later, but this is impractical.) (b) In the .4 seconds the arrow travels, a deer, traveling at 20mph or 29.33ft/s, can travel 11.7ft. So she needs to lead the deer by 11.7ft.
41.

The position function is $\vec{r}(t)=\left\langle 220t,-16t^{2}+1000\right\rangle$ . The $y$ -component is 0 when $t=7.9$ ; $\vec{r}(7.9)=\left\langle 1739.25,0\right\rangle$ , meaning the box will travel about 1740ft horizontally before it lands.

Exercises 12.4

1.

1
3.

$\vec{T}(t)$ and $\vec{N}(t)$ .
5.
$\vec{T}(t)=\left\langle\frac{4t}{\sqrt{20t^{2}-4t+1}},\frac{2t-1}{\sqrt{20t^{2% }-4t+1}}\right\rangle$ ; $\vec{T}(1)=\left\langle 4/\sqrt{17},1/\sqrt{17}\right\rangle$
7.

$\vec{T}(t)=\frac{\cos t\sin t}{\sqrt{\cos^{2}t\sin^{2}t}}\left\langle-\cos t,% \sin t\right\rangle$ . (Be careful; this cannot be simplified as just $\left\langle-\cos t,\sin t\right\rangle$ as $\sqrt{\cos^{2}t\sin^{2}t}\neq\cos t\sin t$ , but rather $\left\lvert\cos t\sin t\right\rvert$ .) $\vec{T}(\pi/4)=\left\langle-\sqrt{2}/2,\sqrt{2}/2\right\rangle$
9.

$\ell(t)=\left\langle 2,0\right\rangle+t\left\langle 4/\sqrt{17},1/\sqrt{17}\right\rangle$ ; in parametric form,

$\ell(t)=\begin{cases}x=2+4t/\sqrt{17}\\ y=t/\sqrt{17}\end{cases}$
11.

$\ell(t)=\left\langle\sqrt{2}/4,\sqrt{2}/4\right\rangle+t\left\langle-\sqrt{2}/% 2,\sqrt{2}/2\right\rangle$ ; in parametric form,

$\ell(t)=\begin{cases}x=\sqrt{2}/4-\sqrt{2}t/2\\ y=\sqrt{2}/4+\sqrt{2}t/2\end{cases}$
13.

$\vec{T}(t)=\left\langle-\sin t,\cos t\right\rangle$ ; $\vec{N}(t)=\left\langle-\cos t,-\sin t\right\rangle$
15.
$\vec{T}(t)=\left\langle-\frac{\sin t}{\sqrt{4\cos^{2}t+\sin^{2}t}},\frac{2\cos t% }{\sqrt{4\cos^{2}t+\sin^{2}t}}\right\rangle$ ; $\vec{N}(t)=\left\langle-\frac{2\cos t}{\sqrt{4\cos^{2}t+\sin^{2}t}},-\frac{% \sin t}{\sqrt{4\cos^{2}t+\sin^{2}t}}\right\rangle$
17.
(a) Be sure to show work (b) $\vec{N}(\pi/4)=\left\langle-5/\sqrt{34},-3/\sqrt{34}\right\rangle$
19.
(a) Be sure to show work (b) $\vec{N}(0)=\left\langle-\frac{1}{\sqrt{5}},\frac{2}{\sqrt{5}}\right\rangle$
21.

$\vec{T}(t)=\frac{1}{\sqrt{5}}\left\langle 2,\cos t,-\sin t\right\rangle$ ; $\vec{N}(t)=\left\langle 0,-\sin t,-\cos t\right\rangle$
23.
$\vec{T}(t)=\frac{1}{\sqrt{a^{2}+b^{2}}}\left\langle-a\sin t,a\cos t,b\right\rangle$ ; $\vec{N}(t)=\left\langle-\cos t,-\sin t,0\right\rangle$
25.
$a_{\text{T}}=\frac{4t}{\sqrt{1+4t^{2}}}$ and $a_{\text{N}}=\sqrt{4-\frac{16t^{2}}{1+4t^{2}}}$ At $t=0$ , $a_{\text{T}}=0$ and $a_{\text{N}}=2$ ; At $t=1$ , $a_{\text{T}}=4/\sqrt{5}$ and $a_{\text{N}}=2/\sqrt{5}$ . At $t=0$ , all acceleration comes in the form of changing the direction of velocity and not the speed; at $t=1$ , more acceleration comes in changing the speed than in changing direction.
27.
$a_{\text{T}}=0$ and $a_{\text{N}}=2$ At $t=0$ , $a_{\text{T}}=0$ and $a_{\text{N}}=2$ ; At $t=\pi/2$ , $a_{\text{T}}=0$ and $a_{\text{N}}=2$ . The object moves at constant speed, so all acceleration comes from changing direction, hence $a_{\text{T}}=0$ . $\vec{a}(t)$ is always parallel to $\vec{N}(t)$ , but twice as long, hence $a_{\text{N}}=2$ .
29.
$a_{\text{T}}=0$ and $a_{\text{N}}=a$ At $t=0$ , $a_{\text{T}}=0$ and $a_{\text{N}}=a$ ; At $t=\pi/2$ , $a_{\text{T}}=0$ and $a_{\text{N}}=a$ . The object moves at constant speed, meaning that $a_{\text{T}}$ is always 0. The object “rises” along the $z$ -axis at a constant rate, so all acceleration comes in the form of changing direction circling the $z$ -axis. The greater the radius of this circle the greater the acceleration, hence $a_{\text{N}}=a$ .

Exercises 12.5

1.

time and/or distance
3.

Answers may include lines, circles, helixes
5.

$\kappa$
7.

$s=3t$ , so $\vec{r}(s)=\left\langle 2s/3,s/3,-2s/3\right\rangle$
9.
$s=\sqrt{13}t$ , so $\vec{r}(s)=\left\langle 3\cos(s/\sqrt{13}),3\sin(s/\sqrt{13}),2s/\sqrt{13}\right\rangle$
11.

$\kappa=\frac{\left\lvert 6x\right\rvert}{\left(1+(3x^{2}-1)^{2}\right)^{3/2}}$ ;

$\kappa(0)=0$ , $\kappa(1/2)=\frac{192}{17\sqrt{17}}\approx 2.74$ .
13.

$\kappa=\frac{\left\lvert\cos x\right\rvert}{\left(1+\sin^{2}x\right)^{3/2}}$ ;

$\kappa(0)=1$ , $\kappa(\pi/2)=0$
15.

$\kappa=\frac{\left\lvert 2\cos t\cos(2t)+4\sin t\sin(2t)\right\rvert}{\left(4% \cos^{2}(2t)+\sin^{2}t\right)^{3/2}}$ ;

$\kappa(0)=1/4$ , $\kappa(\pi/4)=8$
17.

$\kappa=\frac{\left\lvert 6t^{2}+2\right\rvert}{\left(4t^{2}+(3t^{2}-1)^{2}% \right)^{3/2}}$ ;

$\kappa(0)=2$ , $\kappa(5)=\frac{19}{1394\sqrt{1394}}\approx 0.0004$
19.

$\kappa=0$ ;

$\kappa(0)=0$ , $\kappa(1)=0$
21.

$\kappa=\frac{3}{13}$ ;

$\kappa(0)=3/13$ , $\kappa(\pi/2)=3/13$
23.

maximized at $x=\pm\frac{\sqrt{2}}{\sqrt[4]{5}}$
25.

maximized at $t=1/4$
27.

radius of curvature is $5\sqrt{5}/4$ .
29.

radius of curvature is $9$ .
31.
$x^{2}+(y-1/2)^{2}=1/4$ , or $\vec{c}(t)=\left\langle 1/2\cos t,1/2\sin t+1/2\right\rangle$
33.

$x^{2}+(y+8)^{2}=81$ , or $\vec{c}(t)=\left\langle 9\cos t,9\sin t-8\right\rangle$
35.

Let $\vec{r}(t)=\left\langle x(t),y(t),0\right\rangle$ and apply the second formula of part 3.