12.4 Unit Tangent and Normal Vectors
Unit Tangent Vector
Given a smooth vector-valued function , we defined in Definition 12.2.4 that any vector parallel to is tangent to the graph of at . It is often useful to consider just the direction of and not its magnitude. Therefore we are interested in the unit vector in the direction of . This leads to a definition.
Definition 12.4.1 Unit Tangent Vector
Let be a smooth function on an open interval . The unit tangent vector is
Example 12.4.1 Computing the unit tangent vector
Let . Find and compute and .
SolutionWe apply Definition 12.4.1 to find .
We can now easily compute and :
These are plotted in Figure 12.4.1 with their initial points at and , respectively. (They look rather “short” since they are only length 1.)
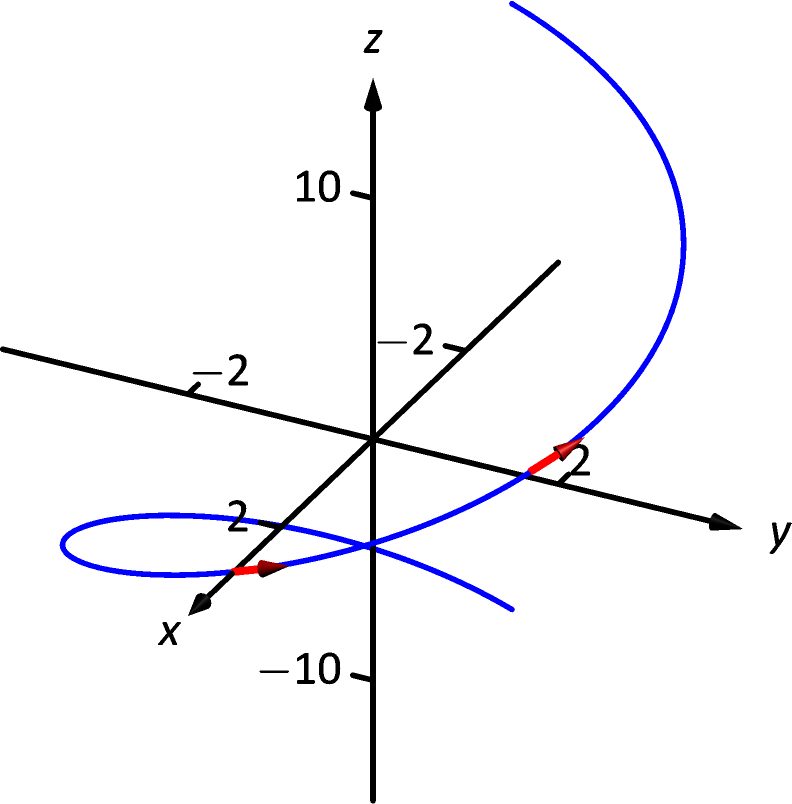 Figure 12.4.1: Plotting unit tangent vectors in Example 12.4.1.
Figure 12.4.1: Plotting unit tangent vectors in Example 12.4.1.
In many ways, the previous example was “too nice.” It turned out that was always of length 5. In the next example the length of is variable, leaving us with a formula that is not as clean.
Example 12.4.2 Computing the unit tangent vector
Let . Find and compute and .
SolutionWe find , and ††margin: Figure 12.4.2: Plotting unit tangent vectors in Example 12.4.2.
Therefore
When , we have ; when , we have We leave it to the reader to verify each of these is a unit vector. They are plotted in Figure 12.4.2
Unit Normal Vector
Just as knowing the direction tangent to a path is important, knowing a direction orthogonal to a path is important. When dealing with real-valued functions, we defined the normal line at a point to the be the line through the point that was perpendicular to the tangent line at that point. We can do a similar thing with vector-valued functions. Given in , we have 2 directions perpendicular to the tangent vector, as shown in Figure 12.4.3. It is good to wonder “Is one of these two directions preferable over the other?”
Given in , there are infinite vectors orthogonal to the tangent vector at a given point. Again, we might wonder “Is one of these infinite choices preferable over the others? Is one of these the ‘right’ choice?”
The answer in both and is “Yes, there is one vector that is preferable.” Recall Theorem 12.2.5, which states that if has constant length, then is orthogonal to for all . We know , the unit tangent vector, has constant length. Therefore is orthogonal to .
We’ll see that is more than just a convenient choice of vector that is orthogonal to ; rather, it is the “right” choice. Since all we care about is the direction, we define this newly found vector to be a unit vector. ††margin: Note: is a unit vector, by definition. This does not imply that is also a unit vector.
Definition 12.4.2 Unit Normal Vector
Let be a vector-valued function where the unit tangent vector, , is smooth on an open interval . The unit normal vector is
Example 12.4.3 Computing the unit normal vector
Let as in Example 12.4.1. Sketch both and with initial points at .
SolutionIn Example 12.4.1, we found . Therefore
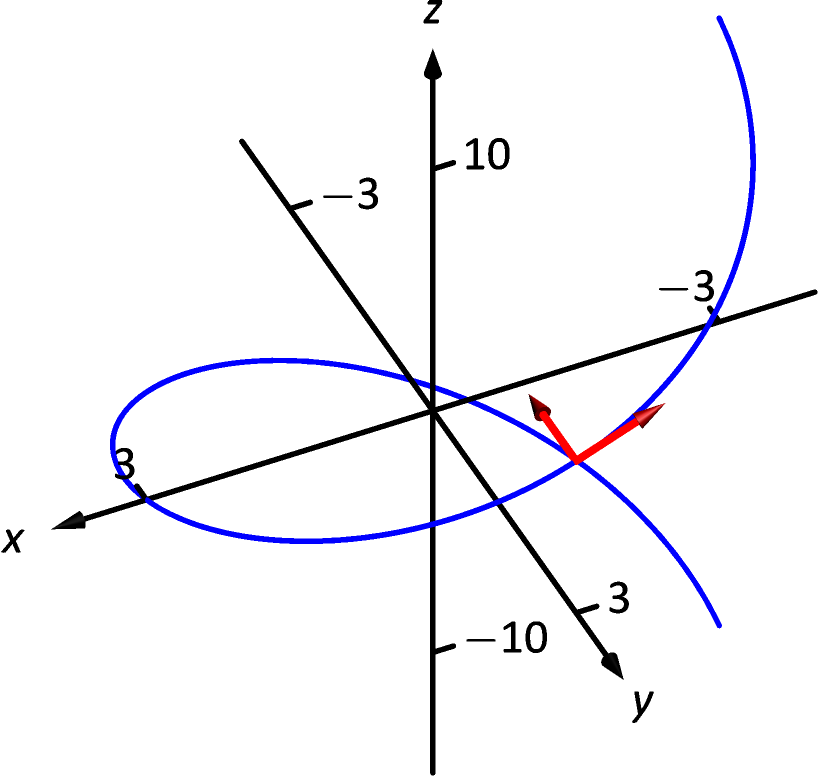 Figure 12.4.4: Plotting unit tangent and normal vectors in Example 12.4.3.
Figure 12.4.4: Plotting unit tangent and normal vectors in Example 12.4.3.
Thus
We compute and . These are sketched in Figure 12.4.4.
The previous example was once again “too nice.” In general, the expression for contains fractions of square-roots, hence the expression of is very messy. We demonstrate this in the next example.
Example 12.4.4 Computing the unit normal vector
Let as in Example 12.4.2. Find and sketch with the unit tangent and normal vectors at and 1.
This is not a unit vector; to find , we need to divide by it’s magnitude.
Finally,
Because we are normalizing , it is usually easier to scale it first. We see that is parallel to , which has length , leading to the same .
Using this formula for , we compute the unit tangent and normal vectors for and 1 and sketch them in Figure 12.4.5.
The final result for in Example 12.4.4 is suspiciously similar to . There is a clear reason for this. If is a unit vector in , then the only unit vectors orthogonal to are and . Given , we can quickly determine if we know which term to multiply by .
Consider again Figure 12.4.5, where we have plotted some unit tangent and normal vectors. Note how always points “inside” the curve, or to the concave side of the curve. This is not a coincidence; this is true in general. Knowing the direction that “turns” allows us to quickly find .
Theorem 12.4.1 Unit Normal Vectors in
Let be a vector-valued function in where is smooth on an open interval . Let be in and Then is either
whichever is the vector that points to the concave side of the graph of .
Application to Acceleration
Let be a position function. It is a fact (stated later in Theorem 12.4.2) that acceleration, , lies in the plane defined by and . That is, there are scalars and such that
The scalar measures “how much” acceleration is in the direction of travel, that is, it measures the component of acceleration that affects the speed. The scalar measures “how much” acceleration is perpendicular to the direction of travel, that is, it measures the component of acceleration that affects the direction of travel.
We can find using the orthogonal projection of onto (review Definition 11.3.3 in Section 11.3 if needed). Recalling that since is a unit vector, , so we have
Thus the amount of in the direction of is . The same logic gives .
While this is a fine way of computing , there are simpler ways of finding (as finding itself can be complicated). The following theorem gives alternate formulas for and . ††margin: Note: Keep in mind that both and are functions of ; that is, the scalar changes depending on . It is convention to drop the “” notation from and simply write .
Theorem 12.4.2 Acceleration in the Plane Defined by and
Let be a position function with acceleration and unit tangent and normal vectors and . Then lies in the plane defined by and ; that is, there exists scalars and such that
Moreover,
Note the second formula for : . This measures the rate of change of speed, which again is the amount of acceleration in the direction of travel.
-
Proof
We see thatSince and are not parallel, this decomposition is unique and the coefficients tell us and .
Because , Theorem 12.2.5 tells us that and are orthogonal. This means that
Also, the Pythagorean theorem tells us that
Example 12.4.5 Computing and
SolutionThe previous examples give and
We can find and directly with dot products:
Thus , which is clearly the case.
What is the practical interpretation of these numbers? means the object is moving at a constant speed, and hence all acceleration comes in the form of direction change.
Example 12.4.6 Computing and
SolutionThe previous examples give and
While we can compute using , we instead demonstrate using another formula from Theorem 12.4.2.
When , and . We interpret this to mean that at , the particle is acculturating mostly by increasing speed, not by changing direction. As the path near is relatively straight, this should make intuitive sense. Figure 12.4.6 gives a graph of the path for reference. ††margin: Figure 12.4.6: Graphing in Example 12.4.6.
Contrast this with , where and . Here the particle’s speed is not changing and all acceleration is in the form of direction change.
Example 12.4.7 Analyzing projectile motion
A ball is thrown from a height of 240ft with an initial speed of 64ft/s and an angle of elevation of . Find the position function of the ball and analyze and .
SolutionUsing Equation (12.1) of Section 12.3 we form the position function of the ball:
which we plot in Figure 12.4.7.
From this we find and . Computing is not difficult, and with some simplification we find
With as simple as it is, finding is also simple:
We choose to not find and find through the formula :
Figure 12.4.8 gives a table of values of and . When , we see the ball’s speed is decreasing; when the speed of the ball is unchanged. This corresponds to the fact that at the ball reaches its highest point.
After we see that is decreasing in value. This is because as the ball falls, it’s path becomes straighter and most of the acceleration is in the form of speeding up the ball, and not in changing its direction. ††margin: 0 27.7 1 32 2 27.7 3 20.9 4 16 5 12.7 Figure 12.4.8: A table of values of and in Example 12.4.7.
Our understanding of the unit tangent and normal vectors is aiding our understanding of motion. The work in Example 12.4.7 gave quantitative analysis of what we intuitively knew.
The next section provides two more important steps towards this analysis. We currently describe position only in terms of time. In everyday life, though, we often describe position in terms of distance (“The gas station is about 2 miles ahead, on the left.”). The arc length parameter allows us to reference position in terms of distance traveled.
We also intuitively know that some paths are straighter than others — and some are curvier than others, but we lack a measurement of “curviness.” The arc length parameter provides a way for us to compute curvature, a quantitative measurement of how curvy a curve is.
Exercises 12.4
Terms and Concepts
-
1.
If is a unit tangent vector, what is ?
-
2.
If is a unit normal vector, what is ?
-
3.
The acceleration vector lies in the plane defined by what two vectors?
-
4.
measures how much the acceleration is affecting the of an object.
Problems
In Exercises 5–8, given , find and evaluate it at the indicated value of .
-
5.
,
-
6.
,
-
7.
,
-
8.
,
In Exercises 9–12, find the equation of the line tangent to the curve at the indicated -value using the unit tangent vector. Note: these are the same problems as in Exercises 5–8.
-
9.
,
-
10.
,
-
11.
,
-
12.
,
In Exercises 13–16, find using Definition 12.4.2. Confirm the result using Theorem 12.4.1.
-
13.
-
14.
-
15.
-
16.
In Exercises 17–20, a position function is given along with its unit tangent vector evaluated at , for some value of .
-
(a)
Confirm that is as stated.
-
(b)
Using a graph of and Theorem 12.4.1, find .
-
17.
; .
-
18.
; .
-
19.
; .
-
20.
; .
In Exercises 21–24, find .
-
21.
-
22.
-
23.
;
-
24.
In Exercises 25–30, find and given . Sketch on the indicated interval, and comment on the relative sizes of and at the indicated values.
-
25.
on ; consider and .
-
26.
on ; consider and .
-
27.
on ; consider and .
-
28.
on ; consider and .
-
29.
on , where ; consider and .
-
30.
on ; consider and .
