13 Functions of Several Variables 13.4 Differentiability and the Total Differential 13.6 Directional Derivatives

13.5 The Multivariable Chain Rule

The Chain Rule, as learned in Section 2.5, states that $\dfrac{d}{dx}\Big{(}f\big{(}g(x)\big{)}\Big{)}=f\,^{\prime}\big{(}g(x)\big{)}g% \hskip 0.75pt^{\prime}(x)$ . If $t=g(x)$ , we can express the Chain Rule as

\frac{df}{dx}=\frac{df}{dt}\frac{dt}{dx}.

In this section we extend the Chain Rule to functions of more than one variable.

Theorem 13.5.1 Multivariable Chain Rule, Part I

Let $z=f(x,y)$ , $x=g(t)$ and $y=h(t)$ , where $f$ , $g$ and $h$ are differentiable functions. Then $z=f(x,y)=f\big{(}g(t),h(t)\big{)}$ is a function of $t$ , and

\frac{dz}{dt}=\frac{df}{dt}=f_{x}(x,y)\frac{dx}{dt}+f_{y}(x,y)\frac{dy}{dt}=% \frac{\partial f}{\partial x}\frac{dx}{dt}+\frac{\partial f}{\partial y}\frac{% dy}{dt}.

Proof

By definition,

\frac{df}{dt}(x,y)=\lim_{h\to 0}\frac{f(x(t+h),y(t+h))-f(x,y)}{h}.

Let

	$\displaystyle\Delta f$	$\displaystyle=f(x(t+h),y(t+h))-f(x,y),$
	$\displaystyle dx$	$\displaystyle=x(t+h)-x(t),\qquad\text{and}$
	$\displaystyle dy$	$\displaystyle=y(t+h)-y(t).$

Because $f$ is differentiable, Definition 13.4.2 gives us functions $E_{1}$ and $E_{2}$ so that

	$\displaystyle E_{1}dx+E_{2}dy=\Delta f-f_{x}(x,y)dx-f_{y}(x,y)dy,$
	$\displaystyle\lim_{(dx,dy)\to 0}E_{1}=0,\qquad\text{and}\qquad\lim_{(dx,dy)\to 0% }E_{2}=0.$

This means that

	$\displaystyle\frac{df}{dt}(x,y)$	$\displaystyle=\lim_{h\to 0}\frac{f_{x}(x,y)dx+f_{y}(x,y)dy+E_{1}dx+E_{2}dy}{h}$
		$\displaystyle=f_{x}(x,y)\lim_{h\to 0}\frac{dx}{h}+f_{y}(x,y)\lim_{h\to 0}\frac% {dy}{h}$
		$\displaystyle\qquad\qquad\mbox{}+\lim_{h\to 0}E_{1}\lim_{h\to 0}\frac{dx}{h}+% \lim_{h\to 0}E_{2}\lim_{h\to 0}\frac{dy}{h}$
		$\displaystyle=f_{x}(x,y)x^{\prime}(t)+f_{y}(x,y)y^{\prime}(t)+0x^{\prime}(t)+0% y^{\prime}(t).\qed$

It is good to understand what the situation of $z=f(x,y)$ , $x=g(t)$ and $y=h(t)$ describes. We know that $z=f(x,y)$ describes a surface; we also recognize that $x=g(t)$ and $y=h(t)$ are parametric equations for a curve in the $x$ - $y$ plane. Combining these together, we are describing a curve that lies on the surface described by $f$ . The parametric equations for this curve are $x=g(t)$ , $y=h(t)$ and $z=f\big{(}g(t),h(t)\big{)}$ .

^†^†margin:

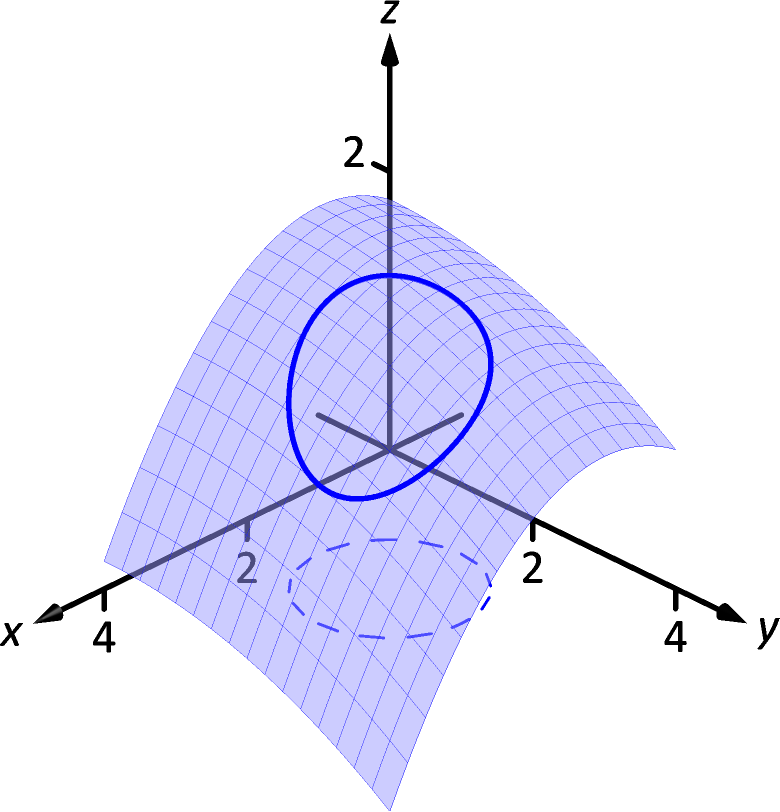Figure 13.5.1: Understanding the application of the Multivariable Chain Rule.

Consider Figure 13.5.1 in which a surface is drawn, along with a dashed curve in the $x$ - $y$ plane. Restricting $f$ to just the points on this circle gives the curve shown on the surface. The derivative $\frac{df}{dt}$ gives the instantaneous rate of change of $f$ with respect to $t$ . If we consider an object traveling along this path, $\frac{df}{dt}$ gives the rate at which the object rises/falls.

We now practice applying the Multivariable Chain Rule.

Example 13.5.1 Using the Multivariable Chain Rule

Let $z=x^{2}y+x$ , where $x=\sin t$ and $y=e^{5t}$ . Find $\displaystyle\frac{dz}{dt}$ using the Chain Rule.

SolutionFollowing Theorem 13.5.1, we find

f_{x}(x,y)=2xy+1,\qquad f_{y}(x,y)=x^{2},\qquad\frac{dx}{dt}=\cos t,\qquad% \frac{dy}{dt}=5e^{5t}.

Applying the theorem, we have

\frac{dz}{dt}=(2xy+1)\cos t+5x^{2}e^{5t}.

This may look odd, as it seems that $\frac{dz}{dt}$ is a function of $x$ , $y$ and $t$ . Since $x$ and $y$ are functions of $t$ , $\frac{dz}{dt}$ is really just a function of $t$ , and we can replace $x$ with $\sin t$ and $y$ with $e^{5t}$ :

\frac{dz}{dt}=(2xy+1)\cos t+5x^{2}e^{5t}=(2\sin(t)e^{5t}+1)\cos t+5e^{5t}\sin^% {2}t.

The previous example can make us wonder: if we substituted for $x$ and $y$ at the end to show that $\frac{dz}{dt}$ is really just a function of $t$ , why not substitute before differentiating, showing clearly that $z$ is a function of $t$ ?

That is, $z=x^{2}y+x=(\sin t)^{2}e^{5t}+\sin t.$ Applying the Chain and Product Rules, we have

\frac{dz}{dt}=2\sin t\cos t\,e^{5t}+5\sin^{2}t\,e^{5t}+\cos t,

which matches the result from the example.

This may now make one wonder “What’s the point? If we could already find the derivative, why learn another way of finding it?” In some cases, applying this rule makes deriving simpler, but this is hardly the power of the Chain Rule. Rather, in the case where $z=f(x,y)$ , $x=g(t)$ and $y=h(t)$ , the Chain Rule is extremely powerful when we do not know what $f$ , $g$ and/or $h$ are. It may be hard to believe, but often in “the real world” we know rate-of-change information (i.e., information about derivatives) without explicitly knowing the underlying functions. The Chain Rule allows us to combine several rates of change to find another rate of change. The Chain Rule also has theoretic use, giving us insight into the behavior of certain constructions (as we’ll see in the next section).

We demonstrate this in the next example.

Example 13.5.2 Applying the Multivariable Chain Rule

An object travels along a path on a surface. The exact path and surface are not known, but at time $t=t_{0}$ it is known that :

\frac{\partial z}{\partial x}=5,\qquad\frac{\partial z}{\partial y}=-2,\qquad% \frac{dx}{dt}=3\qquad\text{and}\qquad\frac{dy}{dt}=7.

Find $\frac{dz}{dt}$ at time $t_{0}$ .

SolutionThe Multivariable Chain Rule states that

	$\displaystyle\frac{dz}{dt}$	$\displaystyle=\frac{\partial z}{\partial x}\frac{dx}{dt}+\frac{\partial z}{% \partial y}\frac{dy}{dt}$
		$\displaystyle=5(3)+(-2)(7)$
		$\displaystyle=1.$

By knowing certain rates-of-change information about the surface and about the path of the particle in the $x$ - $y$ plane, we can determine how quickly the object is rising/falling.

We next apply the Chain Rule to solve a max/min problem.

Example 13.5.3 Applying the Multivariable Chain Rule

Consider the surface $z=x^{2}+y^{2}-xy$ , a paraboloid, on which a particle moves with $x$ and $y$ coordinates given by $x=\cos t$ and $y=\sin t$ . Find $\frac{dz}{dt}$ when $t=0$ , and find where the particle reaches its maximum/minimum $z$ -values.

SolutionIt is straightforward to compute

f_{x}(x,y)=2x-y,\qquad f_{y}(x,y)=2y-x,\qquad\frac{dx}{dt}=-\sin t,\qquad\frac% {dy}{dt}=\cos t.

Combining these according to the Chain Rule gives:

\frac{dz}{dt}=-(2x-y)\sin t+(2y-x)\cos t.

When $t=0$ , $x=1$ and $y=0$ . Thus $\displaystyle\frac{dz}{dt}=-(2)(0)+(-1)(1)=-1$ . When $t=0$ , the particle is moving down, as shown in Figure 13.5.2.

^†^†margin:

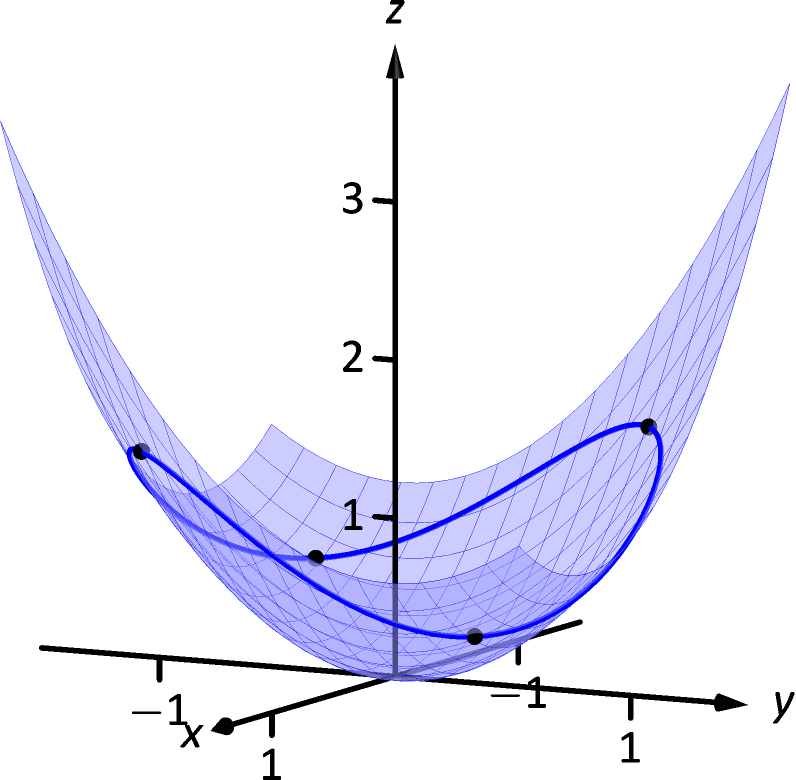Figure 13.5.2: Plotting the path of a particle on a surface in Example 13.5.3.

To find where $z$ -value is maximized/minimized on the particle’s path, we set $\frac{dz}{dt}=0$ and solve for $t$ :

	$\displaystyle\frac{dz}{dt}=0$	$\displaystyle=-(2x-y)\sin t+(2y-x)\cos t$
	$\displaystyle 0$	$\displaystyle=-(2\cos t-\sin t)\sin t+(2\sin t-\cos t)\cos t$
	$\displaystyle 0$	$\displaystyle=\sin^{2}t-\cos^{2}t$
	$\displaystyle\cos^{2}t$	$\displaystyle=\sin^{2}t$
	$\displaystyle t$	$\displaystyle=n\frac{\pi}{4}\quad\text{(for odd $n$)}$

We can use the First Derivative Test to find that on $[0,2\pi]$ , $z$ has reaches its absolute minimum at $t=\pi/4$ and $5\pi/4$ ; it reaches its absolute maximum at $t=3\pi/4$ and $7\pi/4$ , as shown in Figure 13.5.2.

We can extend the Chain Rule to include the situation where $z$ is a function of more than one variable, and each of these variables is also a function of more than one variable. The basic case of this is where $z=f(x,y)$ , and $x$ and $y$ are functions of two variables, say $s$ and $t$ .

Theorem 13.5.2 Multivariable Chain Rule, Part II

1.
Let $z=f(x,y)$ , $x=g(s,t)$ and $y=h(s,t)$ , where $f$ , $g$ and $h$ are differentiable functions. Then $z$ is a function of $s$ and $t$ , and
- •
  
  $\displaystyle\frac{\partial z}{\partial s}=\frac{\partial f}{\partial x}\frac{% \partial x}{\partial s}+\frac{\partial f}{\partial y}\frac{\partial y}{% \partial s}$ , and
- •
  
  $\displaystyle\frac{\partial z}{\partial t}=\frac{\partial f}{\partial x}\frac{% \partial x}{\partial t}+\frac{\partial f}{\partial y}\frac{\partial y}{% \partial t}.$
2.

Let $z=f(x_{1},x_{2},\dots,x_{m})$ be a differentiable function of $m$ variables, where each of the $x_{i}$ is a differentiable function of the variables $t_{1},t_{2},\dots,t_{n}$ . Then $z$ is a function of the $t_{i}$ , and

$\frac{\partial z}{\partial t_{i}}=\frac{\partial f}{\partial x_{1}}\frac{% \partial x_{1}}{\partial t_{i}}+\frac{\partial f}{\partial x_{2}}\frac{% \partial x_{2}}{\partial t_{i}}+\dots+\frac{\partial f}{\partial x_{m}}\frac{% \partial x_{m}}{\partial t_{i}}.$

The proof of Part II follows quickly from Part I, because $\frac{\partial}{\partial t_{i}}$ means that we hold the other variables constant and we are back to the one variable case already proved. A helpful way to remember the derivatives is to examine the following chart

Each possible path from $f$ to the variable $t_{i}$ contributes a term to the sum, and each line segment in a path contributes a factor to that term.

Watch the video:
Generalized Chain Rule — Part 1 from https://youtu.be/HOYA0-pOHsg

Example 13.5.4 Using the Multivariable Chain Rule, Part II

Let $z=x^{2}y+x$ , $x=s^{2}+3t$ and $y=2s-t$ . Find $\frac{\partial z}{\partial s}$ and $\frac{\partial z}{\partial t}$ , and evaluate each when $s=1$ and $t=2$ .

SolutionFollowing Theorem 13.5.2, we compute the following partial derivatives:

	$\displaystyle\frac{\partial f}{\partial x}=2xy+1\qquad\qquad\frac{\partial f}{% \partial y}=x^{2},$
	$\displaystyle\frac{\partial x}{\partial s}=2s\qquad\qquad\frac{\partial x}{% \partial t}=3\qquad\qquad\frac{\partial y}{\partial s}=2\qquad\qquad\frac{% \partial y}{\partial t}=-1.$

Thus

	$\displaystyle\displaystyle\frac{\partial z}{\partial s}=(2xy+1)(2s)+(x^{2})(2)% =4xys+2s+2x^{2},\quad\text{and}$
	$\displaystyle\displaystyle\frac{\partial z}{\partial t}=(2xy+1)(3)+(x^{2})(-1)% =6xy-x^{2}+3.$

When $s=1$ and $t=2$ , $x=7$ and $y=0$ , so

\frac{\partial z}{\partial s}=100\qquad\text{and}\qquad\frac{\partial z}{% \partial t}=-46.

Example 13.5.5 Using the Multivariable Chain Rule, Part II

Let $w=xy+z^{2}$ , where $x=t^{2}e^{s}$ , $y=t\cos s$ , and $z=s\sin t$ . Find $\frac{\partial w}{\partial t}$ when $s=0$ and $t=\pi$ .

SolutionFollowing Theorem 13.5.2, we compute the following partial derivatives:

	$\displaystyle\frac{\partial f}{\partial x}=y\qquad\qquad\frac{\partial f}{% \partial y}=x\qquad\qquad\frac{\partial f}{\partial z}=2z,$
	$\displaystyle\frac{\partial x}{\partial t}=2te^{s}\qquad\qquad\frac{\partial y% }{\partial t}=\cos s\qquad\qquad\frac{\partial z}{\partial t}=s\cos t.$

Thus

\displaystyle\frac{\partial w}{\partial t}=y(2te^{s})+x(\cos s)+2z(s\cos t).

When $s=0$ and $t=\pi$ , we have $x=\pi^{2}$ , $y=\pi$ and $z=0$ . Thus

\frac{\partial w}{\partial t}=\pi(2\pi)+\pi^{2}=3\pi^{2}.

Implicit Differentiation

We studied finding $\frac{dy}{dx}$ when $y$ is given as an implicit function of $x$ in detail in Section 2.6. We find here that the Multivariable Chain Rule gives a simpler method of finding $\frac{dy}{dx}$ .

For instance, consider the implicit function $x^{2}y-xy^{3}=3.$ We learned to use the following steps to find $\frac{dy}{dx}$ :

$\displaystyle\frac{d}{dx}\Big{(}x^{2}y-xy^{3}\big{)}$	$\displaystyle=\frac{d}{dx}\Big{(}3\Big{)}$
$\displaystyle 2xy+x^{2}\frac{dy}{dx}-y^{3}-3xy^{2}\frac{dy}{dx}$	$\displaystyle=0$
$\displaystyle\frac{dy}{dx}=-\frac{2xy-y^{3}}{x^{2}-3xy^{2}}.$		(13.2)

Instead of using this method, consider $z=x^{2}y-xy^{3}$ . The implicit function above describes the level curve $z=3$ . Considering $x$ and $y$ as functions of $x$ , the Multivariable Chain Rule states that

\frac{dz}{dx}=\frac{\partial z}{\partial x}\frac{dx}{dx}+\frac{\partial z}{% \partial y}\frac{dy}{dx}.

(13.3)

Since $z$ is constant (in our example, $z=3$ ), $\frac{dz}{dx}=0$ . We also know $\frac{dx}{dx}=1$ . Equation (13.3) becomes

	$\displaystyle 0$	$\displaystyle=\frac{\partial z}{\partial x}(1)+\frac{\partial z}{\partial y}% \frac{dy}{dx}$
	$\displaystyle\frac{dy}{dx}$	$\displaystyle=-\frac{\partial z}{\partial x}\Big{/}\frac{\partial z}{\partial y}$
		$\displaystyle=-\frac{\,f_{x}\,}{f_{y}}.$

Note how our solution for $\frac{dy}{dx}$ in Equation (13.2) is just the negative of the partial derivative of $z$ with respect to $x$ , divided by the partial derivative of $z$ with respect to $y$ .

We state the above as a theorem for two and three variables.

Theorem 13.5.3 Implicit Differentiation

If $f$ is a differentiable function of $x$ and $y$ , where $f(x,y)=c$ defines $y$ as an implicit function of $x$ for some constant $c$ , then

\frac{dy}{dx}=-\frac{f_{x}(x,y)}{f_{y}(x,y)}.

If $f$ is a differentiable function of $x$ , $y$ , and $z$ , where $f(x,y,z)=c$ defines $z$ as an implicit function of $x$ and $y$ for some constant $c$ , then

\frac{\partial z}{\partial x}=-\frac{f_{x}(x,y,z)}{f_{z}(x,y,z)}\qquad\text{% and}\qquad\frac{\partial z}{\partial y}=-\frac{f_{y}(x,y,z)}{f_{z}(x,y,z)}.

We practice using Theorem 13.5.3 by applying it to a problem from Section 2.6.

Example 13.5.6 Implicit Differentiation

Given the implicitly defined function $\sin(x^{2}y^{2})+y^{3}=x+y$ , find $y\hskip 0.75pt^{\prime}$ . Note: this is the same problem as given in Example 2.6.4 of Section 2.6.

SolutionLet $f(x,y)=\sin(x^{2}y^{2})+y^{3}-x-y$ ; the implicitly defined function above is equivalent to $f(x,y)=0$ . We find $\frac{dy}{dx}$ by applying Theorem 13.5.3. We find

f_{x}(x,y)=2xy^{2}\cos(x^{2}y^{2})-1\qquad\text{and}\qquad f_{y}(x,y)=2x^{2}y% \cos(x^{2}y^{2})+3y^{2}-1,

\frac{dy}{dx}=-\frac{2xy^{2}\cos(x^{2}y^{2})+3y^{2}-1}{2x^{2}y\cos(x^{2}y^{2})% -1},

which matches our solution from Example 2.6.4.

Exercises 13.5

Terms and Concepts

1.

Let a level curve of $z=f(x,y)$ be described by $x=g(t)$ , $y=h(t)$ . Explain why $\frac{dz}{dt}=0$ .
2.

Fill in the blank: The single variable Chain Rule states $\displaystyle\frac{d}{dx}\Big{(}f\big{(}g(x)\big{)}\Big{)}=f\,^{\prime}\big{(}% g(x)\big{)}\cdot$ .
3.
Fill in the blank: The Multivariable Chain Rule states $\displaystyle\frac{df}{dt}=\frac{\partial f}{\partial x}\cdot\text{% \text@underline{ }}+\text{\text@underline{ }}\cdot\frac{% dy}{dt}$ .
4.
If $z=f(x,y)$ , where $x=g(t)$ and $y=h(t)$ , we can substitute and write $z$ as an explicit function of $t$ . T/F: Using the Multivariable Chain Rule to find $\frac{dz}{dt}$ is sometimes easier than first substituting and then taking the derivative.
5.

T/F: The Multivariable Chain Rule is only useful when all the related functions are known explicitly.
6.

The Multivariable Chain Rule allows us to compute implicit derivatives easily by just computing two derivatives.

Problems

In Exercises 7–12, functions $z=f(x,y)$ , $x=g(t)$ and $y=h(t)$ are given.

(a)

Use the Multivariable Chain Rule to compute $\displaystyle\frac{dz}{dt}$ .
(b)

Evaluate $\displaystyle\frac{dz}{dt}$ at the indicated $t$ -value.

7.

$z=3x+4y$ , $x=t^{2}$ , $y=2t$ ; $t=1$
8.

$\displaystyle z=x^{2}-y^{2}$ , $x=t$ , $y=t^{2}-1$ ; $t=1$
9.

$\displaystyle z=5x+2y$ , $x=2\cos t+1$ , $y=\sin t-3$ ; $t=\pi/4$
10.

$\displaystyle z=\frac{x}{y^{2}+1}$ , $x=\cos t$ , $y=\sin t$ ; $t=\pi/2$
11.

$\displaystyle z=x^{2}+2y^{2}$ , $x=\sin t$ , $y=3\sin t$ ; $t=\pi/4$
12.

$z=\cos x\sin y$ , $x=\pi t$ , $y=2\pi t+\pi/2$ ; $t=3$

In Exercises 13–18, functions $z=f(x,y)$ , $x=g(t)$ and $y=h(t)$ are given. Find the values of $t$ where $\frac{dz}{dt}=0$ . Note: these are the same surfaces/curves as found in Exercises 7–12.

13.

$\displaystyle z=3x+4y$ , $x=t^{2}$ , $y=2t$
14.

$\displaystyle z=x^{2}-y^{2}$ , $x=t$ , $y=t^{2}-1$
15.

$\displaystyle z=5x+2y$ , $x=2\cos t+1$ , $y=\sin t-3$
16.

$\displaystyle z=\frac{x}{y^{2}+1}$ , $x=\cos t$ , $y=\sin t$
17.

$\displaystyle z=x^{2}+2y^{2}$ , $x=\sin t$ , $y=3\sin t$
18.

$\displaystyle z=\cos x\sin y$ , $x=\pi t$ , $y=2\pi t+\pi/2$

In Exercises 19–22, functions $z=f(x,y)$ , $x=g(s,t)$ and $y=h(s,t)$ are given.

(a)

Use the Multivariable Chain Rule to compute $\displaystyle\frac{\partial z}{\partial s}$ and $\displaystyle\frac{\partial z}{\partial t}$ .
(b)

Evaluate $\displaystyle\frac{\partial z}{\partial s}$ and $\displaystyle\frac{\partial z}{\partial t}$ at the indicated $s$ and $t$ values.

19.

$\displaystyle z=x^{2}y$ , $x=s-t$ , $y=2s+4t$ ; $s=1$ , $t=0$
20.

$\displaystyle z=\cos\big{(}\pi x+\frac{\pi}{2}y\big{)}$ , $x=st^{2}$ , $y=s^{2}t$ ; $s=1$ , $t=1$
21.

$\displaystyle z=x^{2}+y^{2}$ , $x=s\cos t$ , $y=s\sin t$ ; $s=2$ , $t=\pi/4$
22.

$\displaystyle z=e^{-(x^{2}+y^{2})}$ , $x=t$ , $y=st^{2}$ ; $s=1$ , $t=1$

In Exercises 23–26, find $\dfrac{dy}{dx}$ using Implicit Differentiation and Theorem 13.5.3.

23.

$x^{2}\tan y=50$
24.

$(3x^{2}+2y^{3})^{4}=2$
25.

$\displaystyle\frac{x^{2}+y}{x+y^{2}}=17$
26.

$\displaystyle\ln(x^{2}+xy+y^{2})=1$

In Exercises 27–30, find $\displaystyle\frac{dz}{dt}$ , or $\displaystyle\frac{\partial z}{\partial s}$ and $\displaystyle\frac{\partial z}{\partial t}$ , using the supplied information.

27.

$\displaystyle\frac{\partial z}{\partial x}=2$ , $\displaystyle\frac{\partial z}{\partial y}=1$ , $\displaystyle\frac{dx}{dt}=4$ , $\displaystyle\frac{dy}{dt}=-5$
28.

$\displaystyle\frac{\partial z}{\partial x}=1$ , $\displaystyle\frac{\partial z}{\partial y}=-3$ , $\displaystyle\frac{dx}{dt}=6$ , $\displaystyle\frac{dy}{dt}=2$
29.

$\displaystyle\frac{\partial z}{\partial x}=-4$ , $\displaystyle\frac{\partial z}{\partial y}=9$ ,

$\displaystyle\frac{\partial x}{\partial s}=5$ , $\displaystyle\frac{\partial x}{\partial t}=7$ , $\displaystyle\frac{\partial y}{\partial s}=-2$ , $\displaystyle\frac{\partial y}{\partial t}=6$
30.

$\displaystyle\frac{\partial z}{\partial x}=2$ , $\displaystyle\frac{\partial z}{\partial y}=1$ ,

$\displaystyle\frac{\partial x}{\partial s}=-2$ , $\displaystyle\frac{\partial x}{\partial t}=3$ , $\displaystyle\frac{\partial y}{\partial s}=2$ , $\displaystyle\frac{\partial y}{\partial t}=-1$
31.

Suppose $z=f(x,y)$ is differentiable. Express $(x,y)$ in polar coordinates as $x=r\cos\theta$ , $y=r\sin\theta$ . Calculate $\dfrac{\partial z}{\partial\theta}$ .
32.

Suppose $w=g(x,y,z)$ is differentiable. Express $(x,y,z)$ in spherical coordinates as $x=\rho\sin\phi\cos\theta$ , $y=\rho\sin\phi\sin\theta$ , $z=\rho\cos\phi$ . Calculate $\dfrac{\partial w}{\partial\phi}$ .
33.

Suppose the radius of a circular cylinder is increasing at the constant rate of $1/2$ cm/sec while its height is decreasing at the rate of $1/3$ cm/sec. How is the volume of the cylinder changing when the radius $4$ cm and the height is $10$ cm?