13 Functions of Several Variables 13.6 Directional Derivatives 13.8 Extreme Values

13.7 Tangent Lines, Normal Lines, and Tangent Planes

Derivatives and tangent lines go hand-in-hand. Given $y=f(x)$ , the line tangent to the graph of $f$ at $x=x_{0}$ is the line through $\big{(}x_{0},f(x_{0})\big{)}$ with slope $f\,^{\prime}(x_{0})$ ; that is, the slope of the tangent line is the instantaneous rate of change of $f$ at $x_{0}$ .

When dealing with functions of two variables, the graph is no longer a curve but a surface. At a given point on the surface, it seems there are many lines that fit our intuition of being “tangent” to the surface.

^†^†margin:

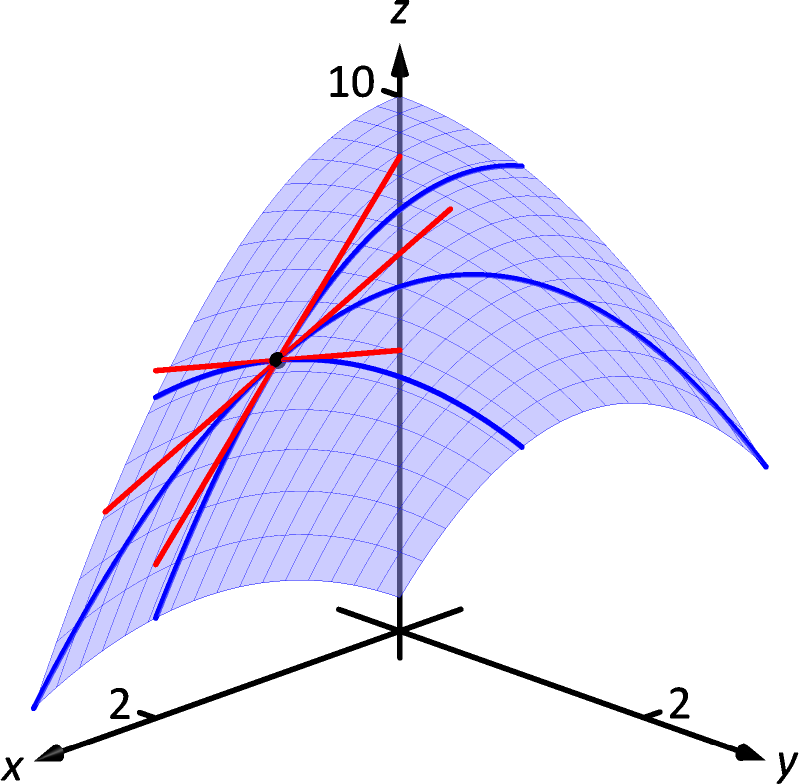Figure 13.7.1: Showing various lines tangent to a surface.

In Figure 13.7.1 we see lines that are tangent to curves in space. Since each curve lies on a surface, it makes sense to say that the lines are also tangent to the surface. The next definition formally defines what it means to be “tangent to a surface.”

Definition 13.7.1 Directional Tangent Line

Let $z=f(x,y)$ be differentiable on an open set $S$ containing $(x_{0},y_{0})$ and let $\vec{u}=\left\langle u_{1},u_{2}\right\rangle$ be a unit vector. The line $\ell_{\vec{u}}$ through $\big{(}x_{0},y_{0},f(x_{0},y_{0})\big{)}$ parallel to $\left\langle u_{1},u_{2},D_{\vec{u}\,}f(x_{0},y_{0})\right\rangle$ is the tangent line to $f$ in the direction of $\vec{u}$ at $(x_{0},y_{0})$ .

We will also follow the convention that

\ell_{\left\langle 1,0\right\rangle}=\ell_{x}\qquad\qquad\text{and}\qquad% \qquad\ell_{\left\langle 0,1\right\rangle}=\ell_{y}.

It is instructive to consider each of three directions given in the definition in terms of “slope.” The direction of $\ell_{x}$ is $\left\langle 1,0,f_{x}(x_{0},y_{0})\right\rangle$ ; that is, the “run” is one unit in the $x$ -direction and the “rise” is $f_{x}(x_{0},y_{0})$ units in the $z$ -direction. Note how the slope is just the partial derivative with respect to $x$ . A similar statement can be made for $\ell_{y}$ . The direction of $\ell_{\vec{u}}$ is $\left\langle u_{1},u_{2},D_{\vec{u}\,}f(x_{0},y_{0})\right\rangle$ ; the “run” is one unit in the $\vec{u}$ direction (where $\vec{u}$ is a unit vector) and the “rise” is the directional derivative of $z$ in that direction.

Definition 13.7.1 leads to the following parametric equations of directional tangent lines:

\displaystyle\ell_{x}(t)=\begin{cases}x=x_{0}+t\\ y=y_{0}\\ z=z_{0}+f_{x}(x_{0},y_{0})t\end{cases}\ \text{,}\quad\ell_{y}(t)=\begin{cases}% x=x_{0}\\ y=y_{0}+t\\ z=z_{0}+f_{y}(x_{0},y_{0})t\end{cases}\ \text{and}\quad\ell_{\vec{u}}(t)=% \begin{cases}x=x_{0}+u_{1}t\\ y=y_{0}+u_{2}t\\ z=z_{0}+D_{\vec{u}\,}f(x_{0},y_{0})t\end{cases}

Watch the video:
Determining a Unit Normal Vector to a Surface from https://youtu.be/DRBNp7SZCvU

Example 13.7.1 Finding directional tangent lines

Find the lines tangent to the surface $z=\sin x\cos y$ at $(\pi/2,\pi/2)$ in the $x$ and $y$ directions and also in the direction of $\vec{v}=\left\langle-1,1\right\rangle.$

SolutionThe partial derivatives with respect to $x$ and $y$ are:

	$\displaystyle f_{x}(x,y)=\cos x\cos y$	$\displaystyle\Rightarrow\quad f_{x}(\pi/2,\pi/2)=0$
	$\displaystyle f_{y}(x,y)=-\sin x\sin y$	$\displaystyle\Rightarrow\quad f_{y}(\pi/2,\pi/2)=-1.$

At $(\pi/2,\pi/2)$ , the $z$ -value is 0.

Thus the parametric equations of the line tangent to $f$ at $(\pi/2,\pi/2)$ in the directions of $x$ and $y$ are: ^†^†margin: 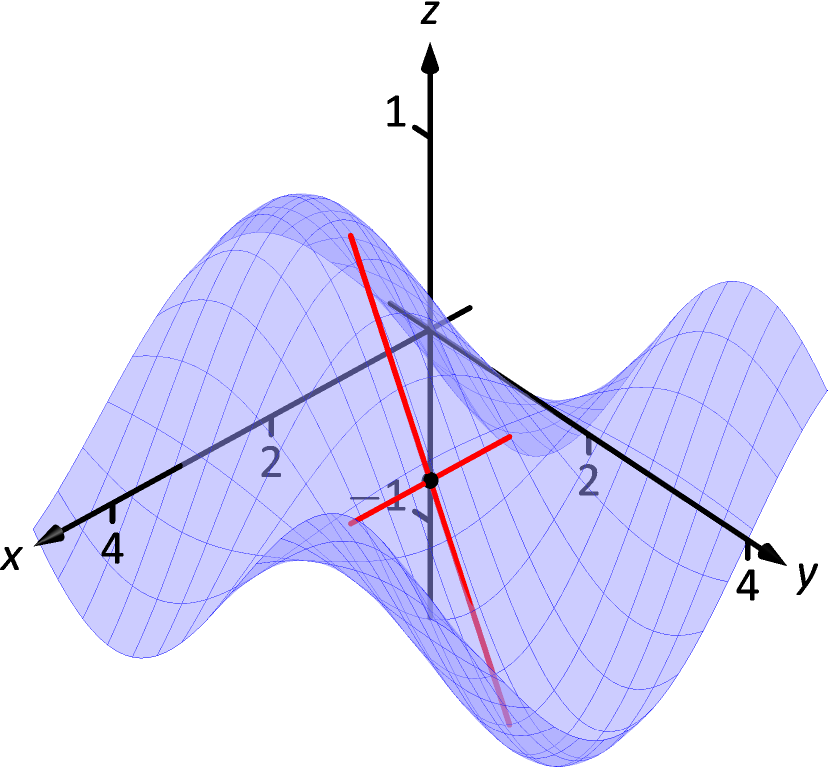(a)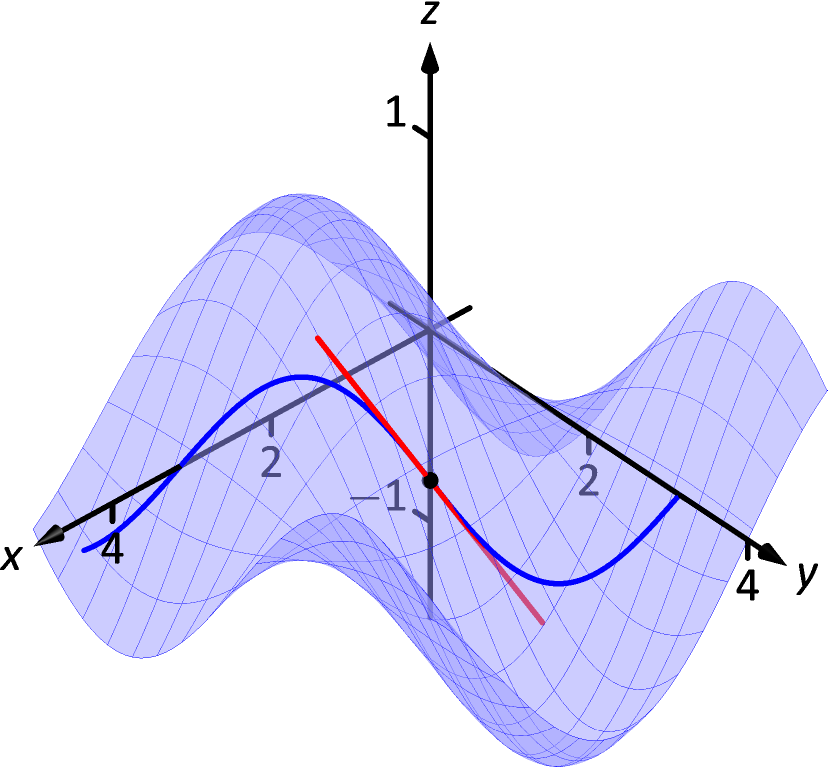 (b) Figure 13.7.2: A surface and directional tangent lines in Example 13.7.1.

\ell_{x}(t)=\begin{cases}x=\pi/2+t\\ y=\pi/2\\ z=0\end{cases}\quad\text{and}\quad\ell_{y}(t)=\begin{cases}x=\pi/2\\ y=\pi/2+t\\ z=-t\end{cases}.

The two lines are shown with the surface in Figure 13.7.2(a). To find the equation of the tangent line in the direction of $\vec{v}$ , we first find the unit vector in the direction of $\vec{v}$ : $\vec{u}=\left\langle-1/\sqrt{2},1/\sqrt{2}\right\rangle$ . The directional derivative at $(\pi/2,\pi,2)$ in the direction of $\vec{u}$ is

D_{\vec{u}\,}f(\pi/2,\pi,2)=\left\langle 0,-1\right\rangle\cdot\left\langle-1/% \sqrt{2},1/\sqrt{2}\right\rangle=-1/\sqrt{2}.

Thus the directional tangent line is

\ell_{\vec{u}}(t)=\begin{cases}x=\pi/2-t/\sqrt{2}\\ y=\pi/2+t/\sqrt{2}\\ z=-t/\sqrt{2}\end{cases}.

The curve through $(\pi/2,\pi/2,0)$ in the direction of $\vec{v}$ is shown in Figure 13.7.2(b) along with $\ell_{\vec{u}}(t)$ .

Example 13.7.2 Finding directional tangent lines

Let $f(x,y)=4xy-x^{4}-y^{4}$ . Find the equations of all directional tangent lines to $f$ at $(1,1)$ .

SolutionFirst note that $f(1,1)=2$ . We need to compute directional derivatives, so we need $\nabla f$ . We begin by computing partial derivatives.

f_{x}=4y-4x^{3}\Rightarrow f_{x}(1,1)=0;\quad f_{y}=4x-4y^{3}\Rightarrow f_{y}% (1,1)=0.

Thus $\nabla f(1,1)=\left\langle 0,0\right\rangle$ . Let $\vec{u}=\left\langle u_{1},u_{2}\right\rangle$ be any unit vector. The directional derivative of $f$ at $(1,1)$ will be $D_{\vec{u}\,}f(1,1)=\left\langle 0,0\right\rangle\cdot\left\langle u_{1},u_{2}% \right\rangle=0$ . It does not matter what direction we choose; the directional derivative is always 0. Therefore ^†^†margin: 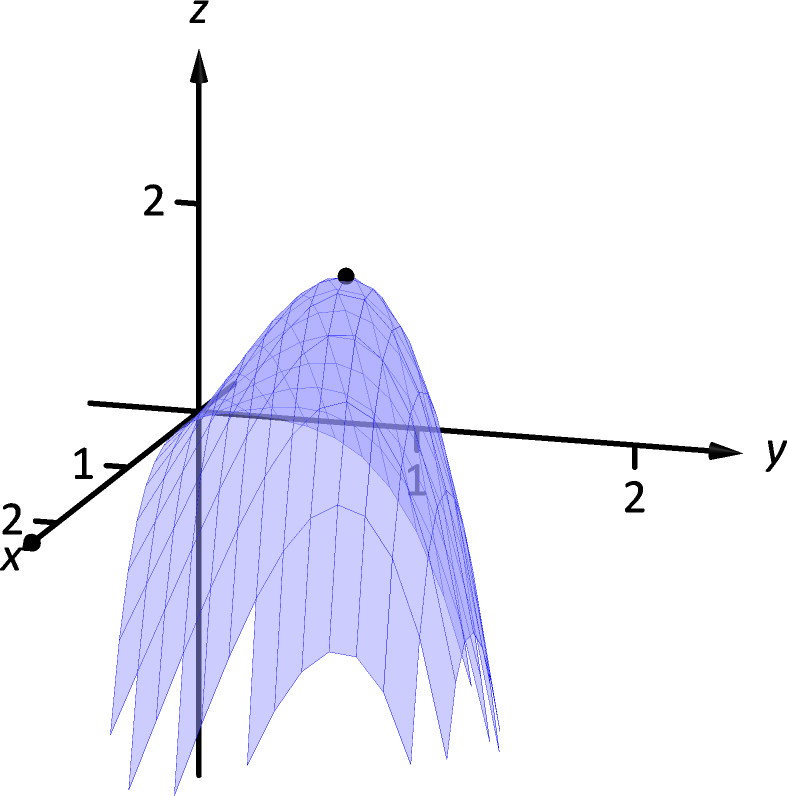Figure 13.7.3: Graphing $f$ in Example 13.7.2.

\ell_{\vec{u}}(t)=\begin{cases}x=1+u_{1}t\\ y=1+u_{2}t\\ z=2\end{cases}.

Figure 13.7.3 shows a graph of $f$ and the point $(1,1,2)$ . Note that this point comes at the top of a “hill,” and therefore every tangent line through this point will have a “slope” of 0.

That is, consider any curve on the surface that goes through this point. Each curve will have a relative maximum at this point, hence its tangent line will have a slope of 0. The following section investigates the points on surfaces where all tangent lines have a slope of 0.

Normal Lines

When dealing with a function $y=f(x)$ of one variable, we stated that a line through $(c,f(c))$ was tangent to $f$ if the line had a slope of $f\,^{\prime}(c)$ and was normal (or, perpendicular, orthogonal) to $f$ if it had a slope of $-1/f\,^{\prime}(c)$ . We extend the concept of normal, or orthogonal, to functions of two variables.

Let $z=f(x,y)$ be a differentiable function of two variables. By Definition 13.7.1, at $(x_{0},y_{0})$ , $\ell_{x}(t)$ is a line parallel to the vector $\vec{d}_{x}=\left\langle 1,0,f_{x}(x_{0},y_{0})\right\rangle$ and $\ell_{y}(t)$ is a line parallel to $\vec{d}_{y}=\left\langle 0,1,f_{y}(x_{0},y_{0})\right\rangle$ . Since lines in these directions through $\big{(}x_{0},y_{0},f(x_{0},y_{0})\big{)}$ are tangent to the surface, a line through this point and orthogonal to these directions would be orthogonal, or normal, to the surface. We can use this direction to create a normal line.

The direction of the normal line is orthogonal to $\vec{d}_{x}$ and $\vec{d}_{y}$ , hence the direction is parallel to $\vec{d}_{n}=\vec{d}_{x}\times\vec{d}_{y}$ . It turns out this cross product has a very simple form:

\vec{d}_{x}\times\vec{d}_{y}=\left\langle 1,0,f_{x}\right\rangle\times\left% \langle 0,1,f_{y}\right\rangle=\left\langle-f_{x},-f_{y},1\right\rangle.

It is often more convenient to refer to the opposite of this direction, namely $\left\langle f_{x},f_{y},-1\right\rangle$ . This leads to a definition.

Definition 13.7.2 Normal Line

Let $z=f(x,y)$ be differentiable on an open set $S$ containing $(x_{0},y_{0})$ .

1.

A nonzero vector parallel to $\vec{n}=\left\langle f_{x}(x_{0},y_{0}),f_{y}(x_{0},y_{0}),-1\right\rangle$ is orthogonal to $f$ at $P=\big{(}x_{0},y_{0},f(x_{0},y_{0})\big{)}$ .
2.

The line $\ell_{n}$ through $P$ with direction parallel to $\vec{n}$ is the normal line to $f$ at $P$ .

Thus the parametric equations of the normal line to a surface $f$ at $\big{(}x_{0},y_{0},f(x_{0},y_{0})\big{)}$ is:

\ell_{n}(t)=\begin{cases}x=x_{0}+f_{x}(x_{0},y_{0})t\\ y=y_{0}+f_{y}(x_{0},y_{0})t\\ z=f(x_{0},y_{0})-t.\end{cases}

Example 13.7.3 Finding a normal line

Find the equation of the normal line to $z=-x^{2}-y^{2}+2$ at $(0,1)$ .

SolutionWe find $z_{x}(x,y)=-2x$ and $z_{y}(x,y)=-2y$ ; at $(0,1)$ , we have $z_{x}=0$ and $z_{y}=-2$ . We take the direction of the normal line, following Definition 13.7.2, to be $\vec{n}=\left\langle 0,-2,-1\right\rangle$ . The line with this direction going through the point $(0,1,1)$ is ^†^†margin: 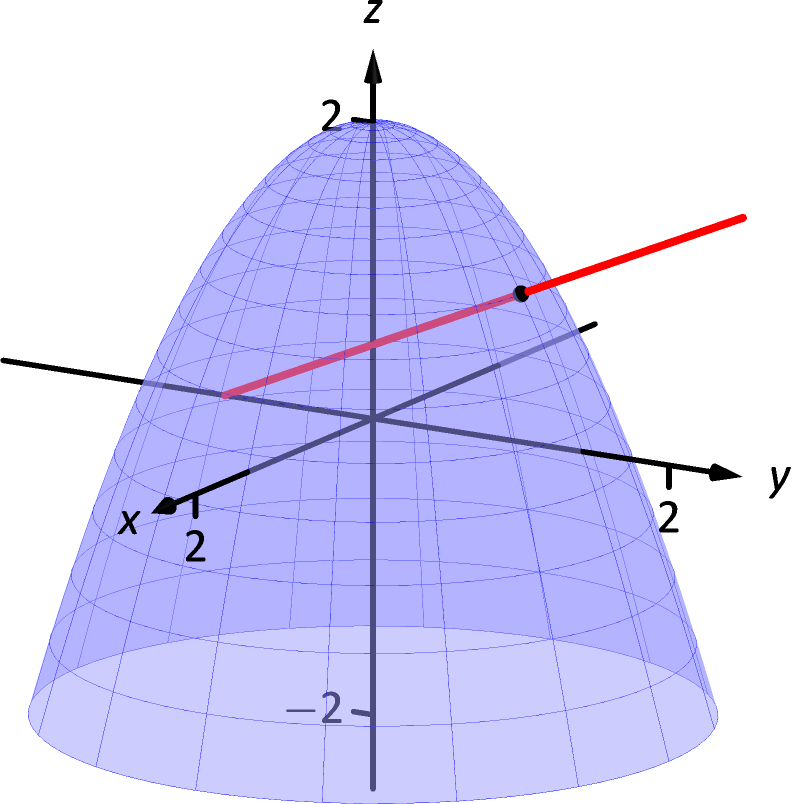Figure 13.7.4: Graphing a surface with a normal line from Example 13.7.3.

\ell_{n}(t)=\begin{cases}x=0\\ y=-2t+1\\ z=-t+1\end{cases}\quad\text{or}\quad\ell_{n}(t)=\left\langle 0,-2,-1\right% \rangle t+\left\langle 0,1,1\right\rangle.

The surface $z=-x^{2}-y^{2}+2$ , along with the found normal line, is graphed in Figure 13.7.4.

The direction of the normal line has many uses, one of which is the definition of the tangent plane which we define shortly. Another use is in measuring distances from the surface to a point. Given a point $Q$ in space, it is a general geometric concept to define the distance from $Q$ to the surface as being the length of the shortest line segment $\overline{PQ}$ over all points $P$ on the surface. This, in turn, implies that $\vec{P}Q$ will be orthogonal to the surface at $P$ . Therefore we can measure the distance from $Q$ to the surface $f$ by finding a point $P$ on the surface such that $\vec{P}Q$ is parallel to the normal line to $f$ at $P$ .

Example 13.7.4 Finding the distance from a point to a surface

Let $f(x,y)=2-x^{2}-y^{2}$ and let $Q=(2,2,2)$ . Find the distance from $Q$ to the surface defined by $f$ .

SolutionThis surface is used in Example 13.7.2, so we know that at $(x,y)$ , the direction of the normal line will be $\vec{d}_{n}=\left\langle-2x,-2y,-1\right\rangle$ . A point $P$ on the surface will have coordinates $(x,y,2-x^{2}-y^{2})$ , so $\vec{P}Q=\left\langle 2-x,2-y,x^{2}+y^{2}\right\rangle$ . To find where $\vec{P}Q$ is parallel to $\vec{d}_{n}$ , we need to find $x$ , $y$ and $c$ such that $c\vec{P}Q=\vec{d}_{n}$ .

	$\displaystyle c\vec{P}Q$	$\displaystyle=\vec{d}_{n}$
	$\displaystyle c\left\langle 2-x,2-y,x^{2}+y^{2}\right\rangle$	$\displaystyle=\left\langle-2x,-2y,-1\right\rangle.$
This implies
	$\displaystyle c(2-x)$	$\displaystyle=-2x$
	$\displaystyle c(2-y)$	$\displaystyle=-2y$
	$\displaystyle c(x^{2}+y^{2})$	$\displaystyle=-1$

In each equation, we can solve for $c$ :

c=\frac{-2x}{2-x}=\frac{-2y}{2-y}=\frac{-1}{x^{2}+y^{2}}.

The first two fractions imply $x=y$ , and so the last fraction can be rewritten as $c=-1/(2x^{2})$ . Then

	$\displaystyle\frac{-2x}{2-x}$	$\displaystyle=\frac{-1}{2x^{2}}$
	$\displaystyle-2x(2x^{2})$	$\displaystyle=-1(2-x)$
	$\displaystyle 4x^{3}$	$\displaystyle=2-x$
	$\displaystyle 4x^{3}+x-2$	$\displaystyle=0.$

Now we consider the cubic polynomial $g(x)=4x^{3}+x-2$ . We have $g(0)=-2<0$ and $g(1)=3>0$ so there is at least one real root by the Intermediate Value Theorem. Since $g^{\prime}(x)=12x^{2}+1>0$ there is at most one real root. Call this unique real root $r$ . Then $P=(r,r,2-2r^{2})$ and so the distance from $Q$ to the surface is

\left\lVert\vec{P}Q\right\rVert=\sqrt{(2-r)^{2}+(2-r)^{2}+(2r^{2})^{2}}.

What is $r$ ? In general it is difficult (or impossible) to find the roots of a polynomial explicitly. In this case we could use the cubic formula (if we happen to know it) to find

r=\frac{1}{2}\left(\sqrt[3]{2+\sqrt{\frac{109}{27}}}+\sqrt[3]{2-\sqrt{\frac{10% 9}{27}}}\right)

but this isn’t an especially useful representation for $r$ . We can approximate $r$ with a numerical technique (like the Bisection or Newton’s Method) or by using whatever algorithm is built into your calculator or favorite computer program. We find $r\approx.689$ . Thus

P\approx(0.689,0.689,1.051)\qquad\text{and}\qquad\left\lVert\vec{P}Q\right% \rVert\approx 2.083.

We can take the concept of measuring the distance from a point to a surface to find a point $Q$ a particular distance from a surface at a given point $P$ on the surface.

Example 13.7.5 Finding a point a set distance from a surface

Let $f(x,y)=x-y^{2}+3$ . Let $P=\big{(}2,1,f(2,1)\big{)}=(2,1,4)$ . Find points $Q$ in space that are 4 units from the surface of $f$ at $P$ . That is, find $Q$ such that $\left\lVert\vec{P}Q\right\rVert=4$ and $\vec{P}Q$ is orthogonal to $f$ at $P$ .

SolutionWe begin by finding partial derivatives:

	$\displaystyle f_{x}(x,y)=1$	$\displaystyle\Rightarrow\qquad f_{x}(2,1)=1$
	$\displaystyle f_{y}(x,y)=-2y$	$\displaystyle\Rightarrow\qquad f_{y}(2,1)=-2$

The vector $\vec{n}=\left\langle 1,-2,-1\right\rangle$ is orthogonal to $f$ at $P$ . For reasons that will become more clear in a moment, we find the unit vector in the direction of $\vec{n}$ :

\vec{u}=\frac{\vec{n}}{\left\lVert\vec{n}\right\rVert}=\frac{\left\langle 1,-2% ,-1\right\rangle}{\sqrt{6}}.

Thus a the normal line to $f$ at $P$ can be written as

\ell_{n}(t)=\left\langle 2,1,4\right\rangle+\frac{t}{\sqrt{6}}\left\langle 1,-% 2,-1\right\rangle.

An advantage of this parameterization of the line is that letting $t=t_{0}$ gives a point on the line that is $\left\lvert t_{0}\right\rvert$ units from $P$ . (This is because the direction of the line is given in terms of a unit vector.) There are thus two points in space 4 units from $P$ : ^†^†margin: 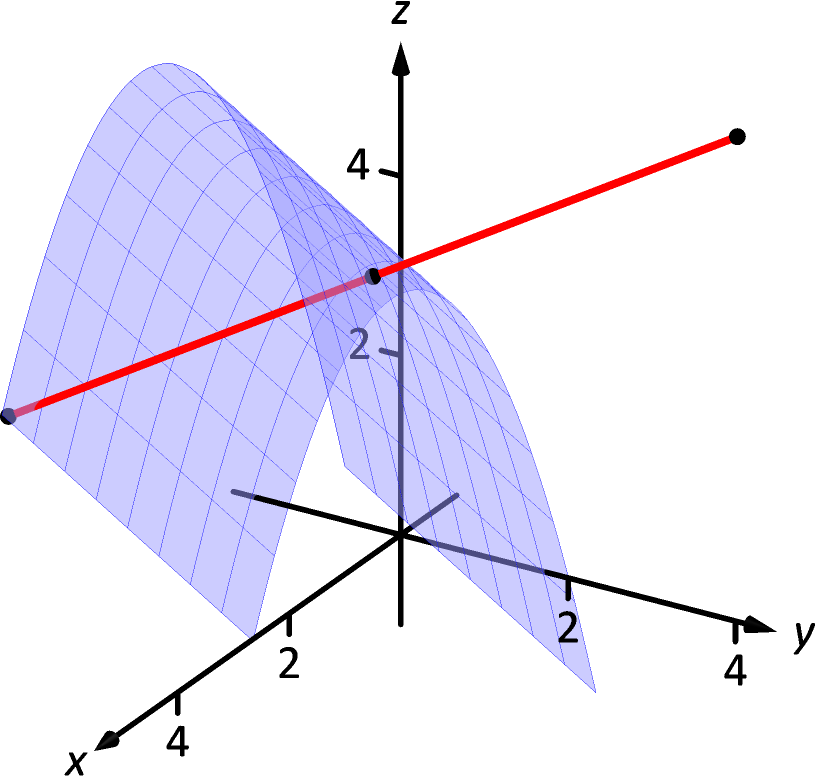Figure 13.7.5: Graphing the surface in Example 13.7.5 along with points 4 units from the surface.

	$\displaystyle Q_{1}$	$\displaystyle=\ell_{n}(4)$	$\displaystyle Q_{2}$	$\displaystyle=\ell_{n}(-4)$
		$\displaystyle=\left\langle 2+\frac{4}{\sqrt{6}},1-\frac{8}{\sqrt{6}},4-\frac{4% }{\sqrt{6}}\right\rangle$		$\displaystyle=\left\langle 2-\frac{4}{\sqrt{6}},1+\frac{8}{\sqrt{6}},4+\frac{4% }{\sqrt{6}}\right\rangle$

The surface is graphed along with points $P$ , $Q_{1}$ , $Q_{2}$ and a portion of the normal line to $f$ at $P$ .

Tangent Planes

We can use the direction of the normal line to define a plane. With $a=f_{x}(x_{0},y_{0})$ , $b=f_{y}(x_{0},y_{0})$ and $P=\big{(}x_{0},y_{0},f(x_{0},y_{0})\big{)}$ , the vector $\vec{n}=\left\langle a,b,-1\right\rangle$ is orthogonal to $f$ at $P$ . The plane through $P$ with normal vector $\vec{n}$ is therefore tangent to $f$ at $P$ .

Definition 13.7.3 Tangent Plane

Let $z=f(x,y)$ be differentiable on an open set $S$ containing $(x_{0},y_{0})$ , where $a=f_{x}(x_{0},y_{0})$ , $b=f_{y}(x_{0},y_{0})$ , $\vec{n}=\left\langle a,b,-1\right\rangle$ and $P=\big{(}x_{0},y_{0},f(x_{0},y_{0})\big{)}$ .

The plane through $P$ with normal vector $\vec{n}$ is the tangent plane to $f$ at $P$ . The standard form of this plane is

a(x-x_{0})+b(y-y_{0})-\big{(}z-f(x_{0},y_{0})\big{)}=0.

Example 13.7.6 Finding tangent planes

Find the equation of the tangent plane to $z=-x^{2}-y^{2}+2$ at $(0,1)$ .

SolutionNote that this is the same surface and point used in Example 13.7.3. ^†^†margin: 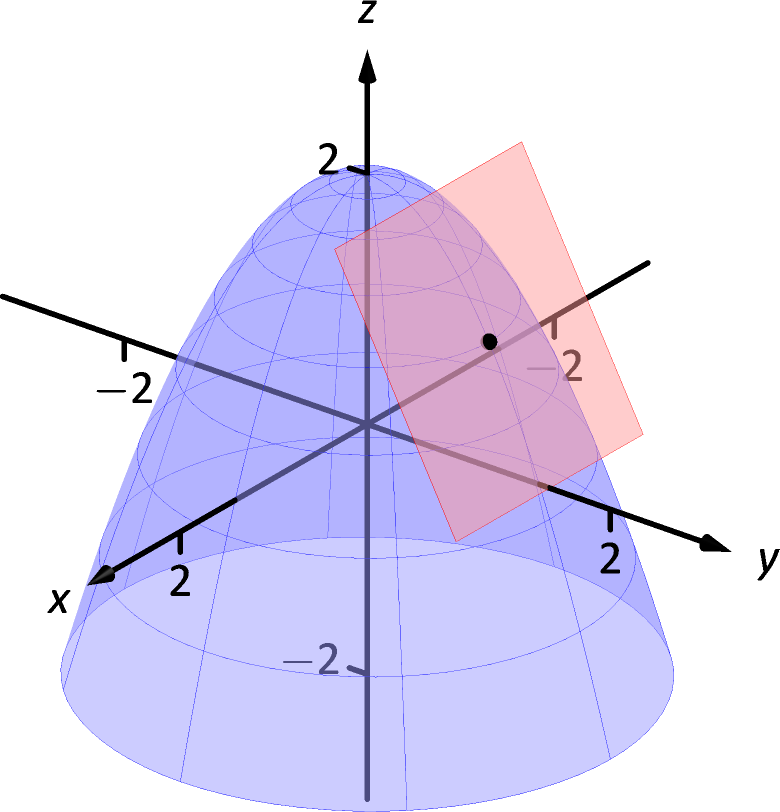Figure 13.7.6: Graphing a surface with tangent plane from Example 13.7.6. There we found $\vec{n}=\left\langle 0,-2,-1\right\rangle$ and $P=(0,1,1)$ . Therefore the equation of the tangent plane is

-2(y-1)-(z-1)=0.

The surface $z=-x^{2}-y^{2}+2$ and tangent plane are graphed in Figure 13.7.6.

Example 13.7.7 Using the tangent plane to approximate function values

The point $(3,-1,4)$ lies on the surface of an unknown differentiable function $f$ where $f_{x}(3,-1)=2$ and $f_{y}(3,-1)=-1/2$ . Find the equation of the tangent plane to $f$ at $P$ , and use this to approximate the value of $f(2.9,-0.8)$ .

SolutionKnowing the partial derivatives at $(3,-1)$ allows us to form the normal vector to the tangent plane, $\vec{n}=\left\langle 2,-1/2,-1\right\rangle$ . Thus the equation of the tangent line to $f$ at $P$ is:

2(x-3)-1/2(y+1)-(z-4)=0\quad\Rightarrow\quad z=2(x-3)-1/2(y+1)+4.

(13.5)

Just as tangent lines provide excellent approximations of curves near their point of intersection, tangent planes provide excellent approximations of surfaces near their point of intersection. So $f(2.9,-0.8)\approx z(2.9,-0.8)=3.7.$

This is not a new method of approximation. Compare the right hand expression for $z$ in Equation (13.5) to the total differential:

dz=f_{x}dx+f_{y}dy\quad\text{and}\quad z=\underbrace{\underbrace{2}_{f_{x}}% \underbrace{(x-3)}_{dx}+\underbrace{-1/2}_{f_{y}}\underbrace{(y+1)}_{dy}}_{dz}% +4.

Thus the “new $z$ -value” is the sum of the change in $z$ (i.e., $d z$ ) and the old $z$ -value (4). As mentioned when studying the total differential, it is not uncommon to know partial derivative information about a unknown function, and tangent planes are used to give accurate approximations of the function.

The Gradient and Normal Lines, Tangent Planes

The methods developed in this section so far give a straightforward method of finding equations of normal lines and tangent planes for surfaces with explicit equations of the form $z=f(x,y)$ . However, they do not handle implicit equations well, such as $x^{2}+y^{2}+z^{2}=1$ . There is a technique that allows us to find vectors orthogonal to these surfaces based on the gradient.

Recall that when $z=f(x,y)$ , the gradient $\nabla f=\left\langle f_{x},f_{y}\right\rangle$ is orthogonal to level curves of $f$ . Theorem 13.6.3 part 3 made an analogous statement about the gradient $\nabla F$ , where $w=F(x,y,z)$ . Given a point $(x_{0},y_{0},z_{0})$ , let $c=F(x_{0},y_{0},z_{0})$ . Then $F(x,y,z)=c$ is a level surface that contains the point $(x_{0},y_{0},z_{0})$ and $\nabla F(x_{0},y_{0},z_{0})$ is orthogonal to this level surface. This direction can be used to find tangent planes and normal lines.

Example 13.7.8 Using the gradient to find a tangent plane

Find the equation of the plane tangent to the ellipsoid $\displaystyle\frac{x^{2}}{12}+\frac{y^{2}}{6}+\frac{z^{2}}{4}=1$ at $P=(1,2,1)$ .

SolutionWe consider the equation of the ellipsoid as a level surface of a function $F$ of three variables, where $F(x,y,z)=\frac{x^{2}}{12}+\frac{y^{2}}{6}+\frac{z^{2}}{4}$ . The gradient is: ^†^†margin: 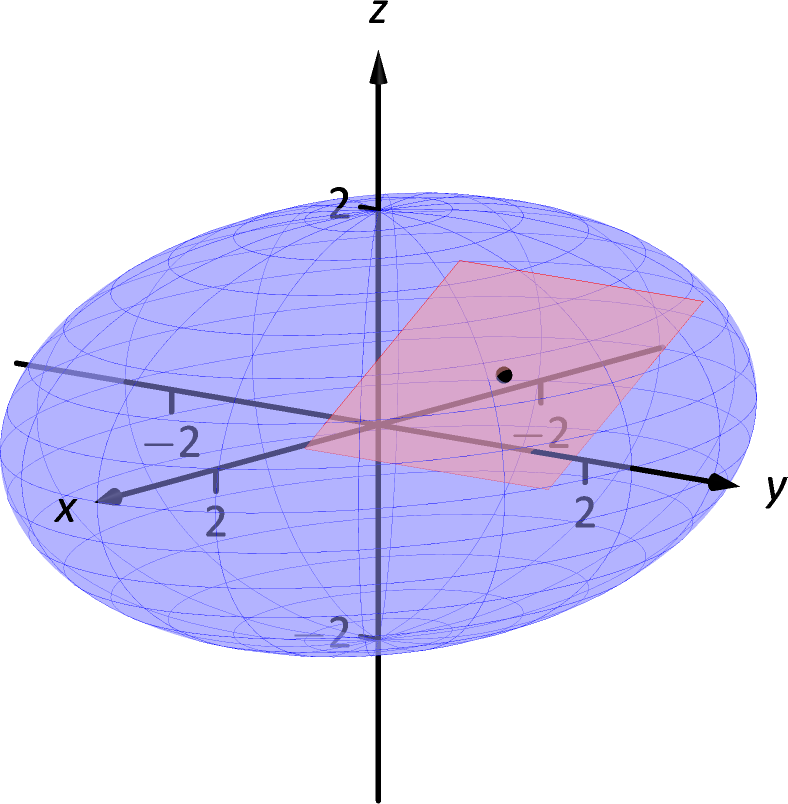Figure 13.7.7: An ellipsoid and its tangent plane at a point.

	$\displaystyle\nabla F(x,y,z)$	$\displaystyle=\left\langle F_{x},F_{y},F_{z}\right\rangle$
		$\displaystyle=\left\langle\frac{x}{6},\frac{y}{3},\frac{z}{2}\right\rangle.$

At $P$ , the gradient is $\nabla F(1,2,1)=\left\langle 1/6,2/3,1/2\right\rangle$ . Thus the equation of the plane tangent to the ellipsoid at $P$ is

\frac{1}{6}(x-1)+\frac{2}{3}(y-2)+\frac{1}{2}(z-1)=0.

The ellipsoid and tangent plane are graphed in Figure 13.7.7.

Taylor Polynomials for Functions of Two Variables

We’ll take a slight detour at this point.

Recall from 9.9.1 that for a function $y=f(x)$ , we have the $n^{\text{th}}$ -order Taylor polynomial about a point $a$ :

p_{n}(x)=\sum_{k=0}^{n}\frac{(x-a)^{k}}{k!}f^{(k)}(a)=p_{n-1}(x)+\frac{(x-a)^{% n}}{n!}f^{(n)}(a),

with an associated remainder $R_{n}(x)=f(x)-p_{n}(x)$ . If we know that $\left\lvert f^{(n+1)}(u)\right\rvert\leq K$ for all $u$ in an open interval containing $a$ and $x$ , then we can bound the remainder as well:

\left\lvert R_{n}(x)\right\rvert\leq K\frac{\left\lvert x-a\right\rvert^{n+1}}% {(n+1)!}.

This section has shown that a function $z=f(x,y)$ can be locally approximated near $(a,b)$ by

L(x,y)=f(a,b)+f_{x}(a,b)(x-a)+f_{y}(a,b)(y-b).

We can combine these ideas and talk about the Taylor polynomial for $f$ (for simplicity, we’ll take $(a,b)=(0,0)$ ). Let

	$\displaystyle{}p_{0}(x,y)$	$\displaystyle=f(0,0)$
	$\displaystyle p_{1}(x,y)$	$\displaystyle=p_{0}(x,y)+xf_{x}(0,0)+yf_{y}(0,0)$
	$\displaystyle p_{2}(x,y)$	$\displaystyle=p_{1}(x,y)+\frac{x^{2}}{2}f_{xx}(0,0)+xyf_{xy}(0,0)+\frac{y^{2}}% {2}(0,0)$
	$\displaystyle p_{3}(x,y)$	$\displaystyle=p_{2}(x,y)+\frac{x^{3}}{3!}f_{xxx}(0,0)+\frac{x^{2}y}{2}f_{xxy}(% 0,0)+\frac{xy^{2}}{2}f_{xyy}(0,0)+\frac{y^{3}}{3!}f_{yyy}(0,0)$
and in general,
	$\displaystyle p_{n}(x,y)$	$\displaystyle=p_{n-1}(x,y)+\sum_{k=0}^{n}\frac{x^{k}y^{n-k}}{k!(n-k)!}\frac{% \partial^{n}f}{\partial x^{k}\partial y^{n-k}}(0,0),$

and define the remainder by $R_{n}(x,y)=f(x,y)-p_{n}(x,y)$ . Notice that each new term in $p_{n}$ consists of all the ways to get a polynomial in $x$ and $y$ of order $n$ along with the unique derivative that would make that polynomial a constant, divided by what that constant would be.

It is also possible to prove a bound on $R_{n}$ . Suppose that

\left\lvert\frac{\partial^{n}f}{\partial x^{k}\partial y^{n-k}}(x,y)\right% \rvert\leq K

for all $k$ and all $(x,y)$ within distance $r$ of the origin. Then for all $(x,y)$ within distance $r$ ,

\left\lvert R_{n-1}(x,y)\right\rvert\leq K\frac{(x^{2}+y^{2})^{n/2}}{n!}\leq K% \frac{r^{n}}{n!}.

Tangent lines and planes to surfaces have many uses, including the study of instantaneous rates of changes and making approximations. Normal lines also have many uses. In this section we focused on using them to measure distances from a surface. Another interesting application is in computer graphics, where the effects of light on a surface are determined using normal vectors.

The next section investigates another use of partial derivatives: determining relative extrema. When dealing with functions of the form $y=f(x)$ , we found relative extrema by finding $x$ where $f\,^{\prime}(x)=0$ . We can start finding relative extrema of $z=f(x,y)$ by setting $f_{x}$ and $f_{y}$ to 0, but it turns out that there is more to consider.

Exercises 13.7

Terms and Concepts

1.

Explain how the vector $\vec{v}=\left\langle 1,0,3\right\rangle$ can be thought of as having a “slope” of 3.
2.

Explain how the vector $\vec{v}=\left\langle 0.6,0.8,-2\right\rangle$ can be thought of as having a “slope” of $-2$ .
3.

T/F: Let $z=f(x,y)$ be differentiable at $P$ . If $\vec{n}$ is a normal vector to the tangent plane of $f$ at $P$ , then $\vec{n}$ is orthogonal to $\ell_{x}$ and $\ell_{y}$ at $P$ .
4.

Explain in your own words why we do not refer to the tangent line to a surface at a point, but rather to directional tangent lines to a surface at a point.

Problems

In Exercises 5–8, a function $z=f(x,y)$ , a vector $\vec{v}$ and a point $P$ are given. Give the parametric equations of the following directional tangent lines to $f$ at $P$ :

(a)

$\ell_{x}(t)$
(b)

$\ell_{y}(t)$
(c)

$\ell_{\vec{u}\,}(t)$ , where $\vec{u}$ is the unit vector in the direction of $\vec{v}$ .

5.

$f(x,y)=2x^{2}y-4xy^{2}$ , $\vec{v}=\left\langle 1,3\right\rangle$ , $P=(2,3)$ .
6.

$f(x,y)=3\cos x\sin y$ , $\vec{v}=\left\langle 1,2\right\rangle$ , $P=(\pi/3,\pi/6)$ .
7.

$f(x,y)=3x-5y$ , $\vec{v}=\left\langle 1,1\right\rangle$ , $P=(4,2)$ .
8.

$f(x,y)=x^{2}-2x-y^{2}+4y$ , $\vec{v}=\left\langle 1,1\right\rangle$ , $P=(1,2)$ .

In Exercises 9–12, a function $z=f(x,y)$ and a point $P$ are given. Find the equation of the normal line to $f$ at $P$ . Note: these are the same functions as in Exercises 5–8.

9.

$f(x,y)=2x^{2}y-4xy^{2}$ , $P=(2,3)$ .
10.

$f(x,y)=3\cos x\sin y$ , $P=(\pi/3,\pi/6)$ .
11.

$f(x,y)=3x-5y$ , $P=(4,2)$ .
12.

$f(x,y)=x^{2}-2x-y^{2}+4y$ , $P=(1,2)$ .

In Exercises 13–16, a function $z=f(x,y)$ and a point $P$ are given. Find the two points that are 2 units from the surface $f$ at $P$ . Note: these are the same functions as in Exercises 5–8.

13.

$f(x,y)=2x^{2}y-4xy^{2}$ , $P=(2,3)$ .
14.

$f(x,y)=3\cos x\sin y$ , $P=(\pi/3,\pi/6)$ .
15.

$f(x,y)=3x-5y$ , $P=(4,2)$ .
16.

$f(x,y)=x^{2}-2x-y^{2}+4y$ , $P=(1,2)$ .

In Exercises 17–20, a function $z=f(x,y)$ and a point $P$ are given. Find the equation of the tangent plane to $f$ at $P$ . Note: these are the same functions as in Exercises 5–8.

17.

$f(x,y)=2x^{2}y-4xy^{2}$ , $P=(2,3)$ .
18.

$f(x,y)=3\cos x\sin y$ , $P=(\pi/3,\pi/6)$ .
19.

$f(x,y)=3x-5y$ , $P=(4,2)$ .
20.

$f(x,y)=x^{2}-2x-y^{2}+4y$ , $P=(1,2)$ .

In Exercises 21–24, an implicitly defined function of $x$ , $y$ and $z$ is given along with a point $P$ that lies on the surface. Use the gradient $\nabla F$ to:

(a)

find the equation of the normal line to the surface at $P$ , and
(b)

find the equation of the plane tangent to the surface at $P$ .

21.

$\displaystyle\frac{x^{2}}{8}+\frac{y^{2}}{4}+\frac{z^{2}}{16}=1$ , at $P=(1,\sqrt{2},\sqrt{6})$
22.

$\displaystyle z^{2}-\frac{x^{2}}{4}-\frac{y^{2}}{9}=0$ , at $P=(4,-3,\sqrt{5})$
23.

$\displaystyle xy^{2}-xz^{2}=0$ , at $P=(2,1,-1)$
24.

$\displaystyle\sin(xy)+\cos(yz)=0$ , at $P=(2,\pi/12,4)$