15 Vector Analysis 15.2 Vector Fields 15.4 Flow, Flux, Green’s Theorem and the Divergence Theorem

15.3 Line Integrals over Vector Fields

Suppose a particle moves along a curve $C$ under the influence of an electromagnetic force described by a vector field $\vec{F}$ . Since a force is inducing motion, work is performed. How can we calculate how much work is performed?

Recall that when moving in a straight line, if $\vec{F}$ represents a constant force and $\vec{d}$ represents the direction and length of travel, then work is simply $W=\vec{F}\cdot\vec{d}$ . However, we generally want to be able to calculate work even if $\vec{F}$ is not constant and $C$ is not a straight line.

As we have practiced many times before, we can calculate work by first approximating, then refining our approximation through a limit that leads to integration.

Assume as we did in Section 15.1 that $C$ can be parameterized by the arc length parameter $s$ . Over a short piece of the curve with length $d s$ , the curve is approximately straight and our force is approximately constant. The straight-line direction of this short length of curve is given by $\vec{T}$ , the unit tangent vector; let $\vec{d}=\vec{T}\ ds$ , which gives the direction and magnitude of a small section of $C$ . Thus work over this small section of $C$ is $\vec{F}\cdot\vec{d}=\vec{F}\cdot\vec{T}\ ds$ .

Summing up all the work over these small segments gives an approximation of the work performed. By taking the limit as $d s$ goes to zero, and hence the number of segments approaches infinity, we can obtain the exact amount of work. Following the logic presented at the beginning of this chapter in the Integration Review, we see that

W=\int_{C}\vec{F}\cdot\vec{T}\ ds,

a line integral.

This line integral is beautiful in its simplicity, yet is not so useful in making actual computations (largely because the arc length parameter is so difficult to work with). To compute actual work, we need to parameterize $C$ with another parameter $t$ via a vector-valued function $\vec{r}(t)$ . As stated in Section 15.1, $ds=\left\lVert\vec{r}\hskip 1.25pt^{\prime}(t)\right\rVert\ dt$ , and recall that $\vec{T}=\vec{r}\hskip 1.25pt^{\prime}(t)/\left\lVert\vec{r}\hskip 1.25pt^{% \prime}(t)\right\rVert$ . Thus

W=\int_{C}\vec{F}\cdot\vec{T}\ ds=\int_{C}\vec{F}\cdot\frac{\vec{r}\hskip 1.25% pt^{\prime}(t)}{\left\lVert\vec{r}\hskip 1.25pt^{\prime}(t)\right\rVert}\left% \lVert\vec{r}\hskip 1.25pt^{\prime}(t)\right\rVert\ dt=\int_{C}\vec{F}\cdot% \vec{r}\hskip 1.25pt^{\prime}(t)\ dt=\int_{C}\vec{F}\cdot d\vec{r},

(15.2)

where the final integral uses the differential $d\vec{r}$ for $\vec{r}\hskip 1.25pt^{\prime}(t)\,dt$ .

These integrals are known as line integrals over vector fields. By contrast, the line integrals we dealt with in Section 15.1 are sometimes referred to as line integrals over scalar fields. Just as a vector field is defined by a function that returns a vector, a scalar field is a function that returns a scalar, such as $z=f(x,y)$ . We waited until now to introduce this terminology so we could contrast the concept with vector fields.

We formally define this line integral, then give examples and applications.

Definition 15.3.1 Line Integral Over A Vector Field

Let $\vec{F}$ be a vector field with continuous components defined on a smooth curve $C$ , parameterized by $\vec{r}(t)$ , and let $\vec{T}$ be the unit tangent vector of $\vec{r}(t)$ . The line integral over $\vec{F}$ along $C$ is

\int_{C}\vec{F}\cdot d\vec{r}=\int_{C}\vec{F}\cdot\vec{T}\ ds.

^†^†margin: Note: When

\vec{F}=\left\langle g,h\right\rangle

and

\vec{r}=\left\langle x,y\right\rangle

parameterizes

C

, other common notations for the line integral over

\vec{F}

along

C

are

\int_{C}gdx+\int_{C}hdy

and

\int_{C}gdx+hdy

In Definition 15.3.1, note how the dot product $\vec{F}\cdot\vec{T}$ is just a scalar. Therefore, this new line integral is really just a special kind of line integral found in Section 15.1; letting $f(s)=\vec{F}(s)\cdot\vec{T}(s)$ , the right-hand side simply becomes $\int_{C}f(s)\ ds$ , and we can use the techniques of that section to evaluate the integral. We combine those techniques, along with parts of Equation (15.2), to clearly state how to evaluate a line integral over a vector field in the following Key Idea.

Key Idea 15.3.1 Evaluating a Line Integral Over A Vector Field

Let $\vec{F}$ be a vector field with continuous components defined on a smooth curve $C$ , parameterized by $\vec{r}(t)$ , $a\leq t\leq b$ , where $\vec{r}$ is continuously differentiable. Then

\int_{C}\vec{F}\cdot\vec{T}\ ds=\int_{C}\vec{F}\cdot d\vec{r}=\int_{a}^{b}\vec% {F}\big{(}\vec{r}(t)\big{)}\cdot\vec{r}\hskip 1.25pt^{\prime}(t)\ dt.

An important concept implicit in this Key Idea: we can use any continuously differentiable parameterization $\vec{r}(t)$ of $C$ that preserves the orientation of $C$ : there isn’t a “right” one. In practice, choose one that seems easy to work with.

Notation note: the above Definition and Key Idea implicitly evaluate $\vec{F}$ along the curve $C$ , which is parameterized by $\vec{r}(t)$ . For instance, if $\vec{F}=\left\langle x+y,x-y\right\rangle$ and $\vec{r}(t)=\left\langle t^{2},\cos t\right\rangle$ , then evaluating $\vec{F}$ along $C$ means substituting the $x$ - and $y$ -components of $\vec{r}(t)$ in for $x$ and $y$ , respectively, in $\vec{F}$ . Therefore, along $C$ , $\vec{F}=\left\langle x+y,x-y\right\rangle=\left\langle t^{2}+\cos t,t^{2}-\cos t\right\rangle$ . Since we are substituting the output of $\vec{r}(t)$ for the input of $\vec{F}$ , we write this as $\vec{F}\big{(}\vec{r}(t)\big{)}$ . This is a slight abuse of notation as technically the input of $\vec{F}$ is to be a point, not a vector, but this shorthand is useful.

We use an example to practice evaluating line integrals over vector fields.

^†^†margin: Figure 15.3.1: Paths through a vector field in Example 15.3.1.

Example 15.3.1 Evaluating a line integral over a vector field: computing work

Two particles move from $(0,0)$ to $(1,1)$ under the influence of the force field $\vec{F}=\left\langle x,x+y\right\rangle$ . One particle follows $C_{1}$ , the line $y=x$ ; the other follows $C_{2}$ , the curve $y=x^{4}$ , as shown in Figure 15.3.1. Force is measured in newtons and distance is measured in meters. Find the work performed by each particle.

SolutionTo compute work, we need to parameterize each path. We use $\vec{r}_{1}(t)=\left\langle t,t\right\rangle$ to parameterize $y=x$ , and let $\vec{r}_{2}(t)=\left\langle t,t^{4}\right\rangle$ parameterize $y=x^{4}$ ; for each, $0\leq t\leq 1$ .

Along the straight-line path, $\vec{F}\big{(}\vec{r}_{1}(t)\big{)}=\left\langle x,x+y\right\rangle=\left% \langle t,t+t\right\rangle=\left\langle t,2t\right\rangle$ . We find $\vec{r}\hskip 1.25pt^{\prime}_{1}(t)=\left\langle 1,2\right\rangle$ . The integral that computes work is:

	$\displaystyle\int_{C_{1}}\vec{F}\cdot d\vec{r}$	$\displaystyle=\int_{0}^{1}\left\langle t,2t\right\rangle\cdot\left\langle 1,1% \right\rangle\ dt$
		$\displaystyle=\int_{0}^{1}3t\ dt$
		$\displaystyle=\frac{3}{2}t^{2}\Big{\|}_{0}^{1}=1.5\text{ joules}.$

Along the curve $y=x^{4}$ , $\vec{F}\big{(}\vec{r}_{2}(t)\big{)}=\left\langle x,x+y\right\rangle=\left% \langle t,t+t^{4}\right\rangle$ . We find $\vec{r}\hskip 1.25pt^{\prime}_{2}(t)=\left\langle 1,4t^{3}\right\rangle$ . The work performed along this path is

	$\displaystyle\int_{C_{2}}\vec{F}\cdot d\vec{r}$	$\displaystyle=\int_{0}^{1}\left\langle t,t+t^{4}\right\rangle\cdot\left\langle 1% ,4t^{3}\right\rangle\ dt$
		$\displaystyle=\int_{0}^{1}\big{(}t+4t^{4}+4t^{7}\big{)}\ dt$
		$\displaystyle=\big{(}\frac{1}{2}t^{2}+\frac{4}{5}t^{5}+\frac{1}{2}t^{8}\big{)}% \Big{\|}_{0}^{1}=1.8\text{ joules}.$

Note how differing amounts of work are performed along the different paths. This should not be too surprising: the force is variable, one path is longer than the other, etc.

^†^†margin: Figure 15.3.2: Paths through a vector field in Example 15.3.2.

Example 15.3.2 Evaluating a line integral over a vector field: computing work

Two particles move from $(-1,1)$ to $(1,1)$ under the influence of a force field $\vec{F}=\left\langle y,x\right\rangle$ . One moves along the curve $C_{1}$ , the parabola defined by $y=2x^{2}-1$ . The other particle moves along the curve $C_{2}$ , the bottom half of the circle defined by $x^{2}+(y-1)^{2}=1$ , as shown in Figure 15.3.2. Force is measured in pounds and distances are measured in feet. Find the work performed by moving each particle along its path.

SolutionWe start by parameterizing $C_{1}$ : the parameterization $\vec{r}_{1}(t)=\left\langle t,2t^{2}-1\right\rangle$ is straightforward, giving $\vec{r}\hskip 1.25pt^{\prime}_{1}=\left\langle 1,4t\right\rangle$ . On $C_{1}$ , $\vec{F}\big{(}\vec{r}_{1}(t)\big{)}=\left\langle y,x\right\rangle=\left\langle 2% t^{2}-1,t\right\rangle$ .

Computing the work along $C_{1}$ , we have:

	$\displaystyle\int_{C_{1}}\vec{F}\cdot d\vec{r}_{1}$	$\displaystyle=\int_{-1}^{1}\left\langle 2t^{2}-1,t\right\rangle\cdot\left% \langle 1,4t\right\rangle\ dt$
		$\displaystyle=\int_{-1}^{1}\big{(}2t^{2}-1+4t^{2}\big{)}\ dt=2\text{ ft-lbs}.$

For $C_{2}$ , it is probably simplest to parameterize the half circle using sine and cosine. Recall that $\vec{r}(t)=\left\langle\cos t,\sin t\right\rangle$ is a parameterization of the unit circle on $0\leq t\leq 2\pi$ ; we add 1 to the second component to shift the circle up one unit, then restrict the domain to $\pi\leq t\leq 2\pi$ to obtain only the lower half, giving $\vec{r}_{2}(t)=\left\langle\cos t,\sin t+1\right\rangle$ , $\pi\leq t\leq 2\pi$ , and hence $\vec{r}\hskip 1.25pt^{\prime}_{2}(t)=\left\langle-\sin t,\cos t\right\rangle$ and $\vec{F}\big{(}\vec{r}_{2}(t)\big{)}=\left\langle y,x\right\rangle=\left\langle% \sin t+1,\cos t\right\rangle$ .

Computing the work along $C_{2}$ , we have:

	$\displaystyle\int_{C_{2}}\vec{F}\cdot d\vec{r}_{2}$	$\displaystyle=\int_{\pi}^{2\pi}\left\langle\sin t+1,\cos t\right\rangle\cdot% \left\langle-\sin t,\cos t\right\rangle\ dt$
		$\displaystyle=\int_{\pi}^{2\pi}\big{(}-\sin^{2}t-\sin t+\cos^{2}t\big{)}\ dt=2% \text{ ft-lbs}.$

Note how the work along $C_{1}$ and $C_{2}$ in this example is the same. We’ll address why later in this section when conservative fields and path independence are discussed.

Properties of Line Integrals Over Vector Fields

Line integrals over vector fields share the same properties as line integrals over scalar fields, with one important distinction. The orientation of the curve $C$ matters with line integrals over vector fields, whereas it did not matter with line integrals over scalar fields.

It is relatively easy to see why. Let $C$ be the unit circle. The area under a surface over $C$ is the same whether we traverse the circle in a clockwise or counterclockwise fashion, hence the line integral over a scalar field on $C$ is the same irrespective of orientation. On the other hand, if we are computing work done by a force field, direction of travel definitely matters. Opposite directions create opposite signs when computing dot products, so traversing the circle in opposite directions will create line integrals that differ by a factor of $-1$ .

Theorem 15.3.1 Properties of Line Integrals Over Vector Fields

1.

Let $\vec{F}$ and $\vec{G}$ be vector fields with continuous components defined on a smooth curve $C$ , parameterized by $\vec{r}(t)$ , and let $k_{1}$ and $k_{2}$ be scalars. Then

$\displaystyle\int_{C}\big{(}k_{1}\vec{F}+k_{2}\vec{G}\big{)}\cdot d\vec{r}=k_{% 1}\int_{C}\vec{F}\cdot d\vec{r}+k_{2}\int_{C}\vec{G}\cdot d\vec{r}.$
2.

Let $C$ be piecewise smooth, composed of smooth components $C_{1}$ and $C_{2}$ . Then

$\int_{C}\vec{F}\cdot d\vec{r}=\int_{C_{1}}\vec{F}\cdot d\vec{r}+\int_{C_{2}}% \vec{F}\cdot d\vec{r}.$
3.

Let $C^{*}$ be the curve $C$ with opposite orientation, parameterized by $\vec{r}\,^{*}$ . Then

$\int_{C}\vec{F}\cdot d\vec{r}=-\int_{C^{*}}\vec{F}\cdot d\vec{r}\,^{*}.$

We demonstrate using these properties in the following example.

^†^†margin: Figure 15.3.3: The vector field and curve in Example 15.3.3.

Example 15.3.3 Using properties of line integrals over vector fields

Let $\vec{F}=\left\langle 3(y-1/2),1\right\rangle$ and let $C$ be the path that starts at $(0,0)$ , goes to $(1,1)$ along the curve $y=x^{3}$ , then returns to $(0,0)$ along the line $y=x$ , as shown in Figure 15.3.3. Evaluate $\oint_{C}\vec{F}\cdot d\vec{r}$ .

SolutionAs $C$ is piecewise smooth, we break it into two components $C_{1}$ and $C_{2}$ , where $C_{1}$ follows the curve $y=x^{3}$ and $C_{2}$ follows the curve $y=x$ .

We parameterize $C_{1}$ with $\vec{r}_{1}(t)=\left\langle t,t^{3}\right\rangle$ on $0\leq t\leq 1$ , with $\vec{r}\hskip 1.25pt^{\prime}_{1}(t)=\left\langle 1,3t^{2}\right\rangle$ . We will use $\vec{F}\big{(}\vec{r}_{1}(t)\big{)}=\left\langle 3(t^{3}-1/2),1\right\rangle$ .

While we always have unlimited ways in which to parameterize a curve, there are 2 “direct” methods to choose from when parameterizing $C_{2}$ . The parameterization $\vec{r}_{2}(t)=\left\langle t,t\right\rangle$ , $0\leq t\leq 1$ traces the correct line segment but with the wrong orientation. Using Property 3 of Theorem 15.3.1, we can use this parameterization and negate the result.

Another choice is to use the techniques of Section 11.5 to create the line with the orientation we desire. We wish to start at $(1,1)$ and travel in the $\vec{d}=\left\langle-1,-1\right\rangle$ direction for one length of $\vec{d}$ , giving equation $\vec{\ell}(t)=\left\langle 1,1\right\rangle+t\left\langle-1,-1\right\rangle=% \left\langle 1-t,1-t\right\rangle$ on $0\leq t\leq 1$ .

Either choice is fine; we choose $\vec{r}_{2}(t)$ to practice using line integral properties. We find $\vec{r}\hskip 1.25pt^{\prime}_{2}(t)=\left\langle 1,1\right\rangle$ and $\vec{F}\big{(}\vec{r}_{2}(t)\big{)}=\left\langle 3(t-1/2),1\right\rangle$ .

Evaluating the line integral (note how we subtract the integral over $C_{2}$ as the orientation of $\vec{r}_{2}(t)$ is opposite):

	$\displaystyle\oint_{C}\vec{F}\cdot d\vec{r}$	$\displaystyle=\int_{C_{1}}\vec{F}\cdot d\vec{r}_{1}-\int_{C_{2}}\vec{F}\cdot d% \vec{r}_{2}$
		$\displaystyle=\int_{0}^{1}\left\langle 3(t^{3}-1/2),1\right\rangle\cdot\left% \langle 1,3t^{2}\right\rangle dt-\int_{0}^{1}\left\langle 3(t-1/2),1\right% \rangle\cdot\left\langle 1,1\right\rangle dt$
		$\displaystyle=\int_{0}^{1}\Big{(}3t^{3}+3t^{2}-3/2\Big{)}\ dt-\int_{0}^{1}\Big% {(}3t-1/2\Big{)}\ dt$
		$\displaystyle=\big{(}1/4\big{)}-\big{(}1\big{)}$
		$\displaystyle=-3/4.$

If we interpret this integral as computing work, the negative work implies that the motion is mostly against the direction of the force, which seems plausible when we look at Figure 15.3.3.

^†^†margin:

Figure 15.3.4: The graph of

\vec{r}(t)

in Example 15.3.4.

Example 15.3.4 Evaluating a line integral over a vector field in space

Let $\vec{F}=\left\langle-y,x,1\right\rangle$ , and let $C$ be the portion of the helix given by $\vec{r}(t)=\left\langle\cos t,\sin t,t/(2\pi)\right\rangle$ on $[0,2\pi]$ , as shown in Figure 15.3.4. Evaluate $\int_{C}\vec{F}\cdot d\vec{r}$ .

SolutionA parameterization is already given for $C$ , so we just need to find $\vec{F}\big{(}\vec{r}(t)\big{)}$ and $\vec{r}\hskip 1.25pt^{\prime}$ (t).

We have $\vec{F}\big{(}\vec{r}(t)\big{)}=\left\langle-\sin t,\cos t,1\right\rangle$ and $\vec{r}\hskip 1.25pt^{\prime}(t)=\left\langle-\sin t,\cos t,1/(2\pi)\right\rangle$ . Thus

	$\displaystyle\int_{C}\vec{F}\cdot d\vec{r}$	$\displaystyle=\int_{0}^{2\pi}\left\langle-\sin t,\cos t,1\right\rangle\cdot% \left\langle-\sin t,\cos t,1/(2\pi)\right\rangle dt$
		$\displaystyle=\int_{0}^{2\pi}\Big{(}\sin^{2}t+\cos^{2}t+\frac{1}{2\pi}\big{)}dt$
		$\displaystyle=2\pi+1\approx 7.28.$

The Fundamental Theorem of Line Integrals

We are preparing to make important statements about the value of certain line integrals over special vector fields. Before we can do that, we need to define some terms that describe the domains over which a vector field is defined.

^†^†margin: Figure 15.3.5:

R_{1}

is simply connected;

R_{2}

is connected, but not simply connected;

R_{3}

is not connected.

A region in the plane is connected if any two points in the region can be joined by a piecewise smooth curve that lies entirely in the region. In Figure 15.3.5, sets $R_{1}$ and $R_{2}$ are connected; set $R_{3}$ is not connected, though it is composed of two connected subregions.

A region is simply connected if every simple closed curve that lies entirely in the region can be continuously deformed (shrunk) to a single point without leaving the region. (A curve is simple if it does not cross itself.) In Figure 15.3.5, only set $R_{1}$ is simply connected. Region $R_{2}$ is not simply connected as any closed curve that goes around the “hole” in $R_{2}$ cannot be continuously shrunk to a single point. As $R_{3}$ is not even connected, it cannot be simply connected, though again it consists of two simply connected subregions.

^†^†margin:

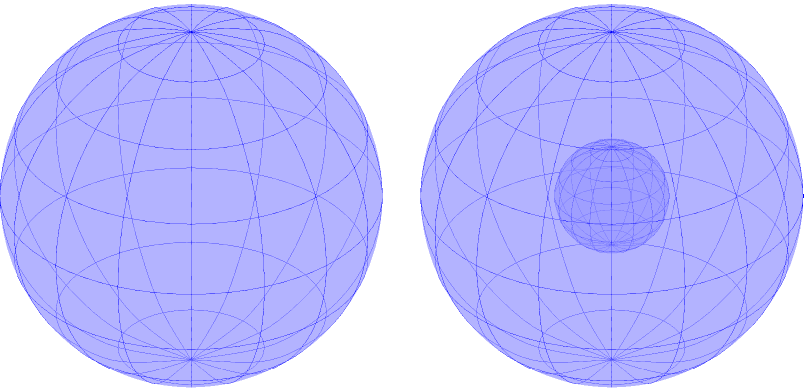(a)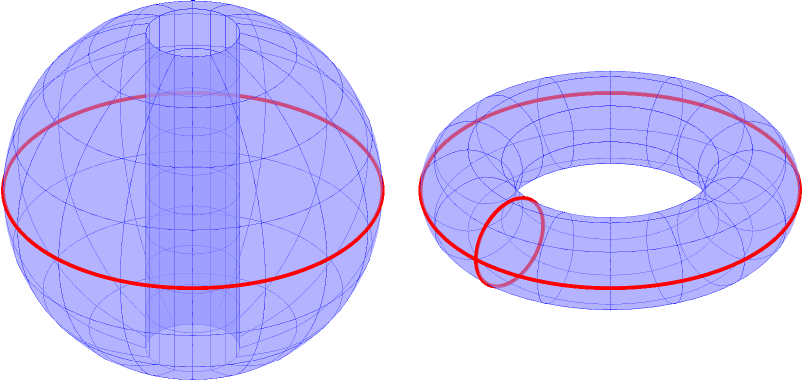

(b) Figure 15.3.6: The domains in (a) are simply connected, while the domains in (b) are not.

We have applied these terms to regions of the plane, but they can be extended intuitively to domains in space (and hyperspace). In Figure 15.3.6(a), the domain bounded by the sphere (at left) and the domain with a subsphere removed (at right) are both simply connected. Any simple closed path that lies entirely within these domains can be continuously deformed into a single point. In Figure 15.3.6(b), neither domain is simply connected. A left, the ball has a hole that extends its length and the pictured closed path cannot be deformed to a point. At right, two paths are illustrated on the torus that cannot be shrunk to a point.

We will use the terms connected and simply connected in subsequent definitions and theorems.

Recall how in Example 15.3.2 particles moved from $A=(-1,1)$ to $B=(1,1)$ along two different paths, wherein the same amount of work was performed along each path. It turns out that regardless of the choice of path from $A$ to $B$ , the amount of work performed under the field $\vec{F}=\left\langle y,x\right\rangle$ is the same. Since our expectation is that differing amounts of work are performed along different paths, we give such special fields a name.

Definition 15.3.2 Conservative Field, Path Independent

Let $\vec{F}$ be a vector field defined on an open, connected domain $D$ in the plane or in space containing points $A$ and $B$ . If the line integral $\int_{C}\vec{F}\cdot d\vec{r}$ has the same value for all choices of paths $C$ starting at $A$ and ending at $B$ , then

•

$\vec{F}$ is a conservative field and
•

The line integral $\int_{C}\vec{F}\cdot d\vec{r}$ is path independent and can be written as

$\int_{C}\vec{F}\cdot d\vec{r}=\int_{A}^{B}\vec{F}\cdot\ d\vec{r}.$

When $\vec{F}$ is a conservative field, the line integral from points $A$ to $B$ is sometimes written as $\int_{A}^{B}\vec{F}\cdot d\vec{r}$ to emphasize the independence of its value from the choice of path; all that matters are the beginning and ending points of the path.

How can we tell if a field is conservative? To show a field $\vec{F}$ is conservative using the definition, we need to show that all line integrals from points $A$ to $B$ have the same value. It is equivalent to show that all line integrals over closed paths $C$ are 0. Each of these tasks are generally nontrivial.

There is a simpler method. Consider the surface defined by $z=f(x,y)=xy$ . We can compute the gradient of this function: $\nabla f=\left\langle f_{x},f_{y}\right\rangle=\left\langle y,x\right\rangle$ . Note that this is the field from Example 15.3.2, which we have claimed is conservative. We will soon give a theorem that states that a field $\vec{F}$ is conservative if, and only if, it is the gradient of some scalar function $f$ . To show $\vec{F}$ is conservative, we need to determine whether or not $\vec{F}=\nabla f$ for some function $f$ . (We’ll later see that there is a yet simpler method). To recognize the special relationship between $\vec{F}$ and $f$ in this situation, $f$ is given a name.

Definition 15.3.3 Potential Function

Let $f$ be a differentiable function defined on a domain $D$ in the plane or in space (i.e., $z=f(x,y)$ or $w=f(x,y,z)$ ) and let $\vec{F}=\nabla f$ , the gradient of $f$ . Then $f$ is a potential function of $\vec{F}$ .

We now state the Fundamental Theorem of Line Integrals, which connects conservative fields and path independence to fields with potential functions.

Theorem 15.3.2 Fundamental Theorem of Line Integrals

Let $\vec{F}$ be a vector field whose components are continuous on a connected domain $D$ in the plane or in space, let $A$ and $B$ be any points in $D$ , and let $C$ be any path in $D$ starting at $A$ and ending at $B$ .

1.

$\vec{F}$ is conservative if and only if there exists a differentiable function $f$ such that $\vec{F}=\nabla f$ .
2.

If $\vec{F}$ is conservative, then

$\int_{C}\vec{F}\cdot d\vec{r}=\int_{A}^{B}\vec{F}\cdot d\vec{r}=f(B)-f(A).$

Once again considering Example 15.3.2, we have $A=(-1,1)$ , $B=(1,1)$ and $\vec{F}=\left\langle y,x\right\rangle$ . In that example, we evaluated two line integrals from $A$ to $B$ and found the value of each was 2. Note that $f(x,y)=xy$ is a potential function for $\vec{F}$ . Following the Fundamental Theorem of Line Integrals, consider $f(B)-f(A)$ :

f(B)-f(A)=f(1,1)-f(-1,1)=1-(-1)=2,

the same value given by the line integrals.

Watch the video:
Ex 1: Fundamental Theorem of Line Integrals — Given Vector Field in a Plane from https://youtu.be/62oBGKSjYiY

We practice using this theorem again in the next example.

Example 15.3.5 Using the Fundamental Theorem of Line Integrals

Let $\vec{F}=\left\langle 3x^{2}y+2x,x^{3}+1\right\rangle$ , $A=(0,1)$ and $B=(1,4)$ . Use the first part of the Fundamental Theorem of Line Integrals to show that $\vec{F}$ is conservative, then choose any path from $A$ to $B$ and confirm the second part of the theorem.

SolutionTo show $\vec{F}$ is conservative, we need to find $z=f(x,y)$ such that $\vec{F}=\nabla f=\left\langle f_{x},f_{y}\right\rangle$ . That is, we need to find $f$ such that $f_{x}=3x^{2}y+2x$ and $f_{y}=x^{3}+1$ . As all we know about $f$ are its partial derivatives, we recover $f$ by integration:

\int\frac{\partial f}{\partial x}\ dx=f(x,y)+C(y).

Note how the constant of integration is more than “just a constant”: it is anything that acts as a constant when taking a derivative with respect to $x$ . Any function that is a function of $y$ (containing no $x$ ’s) acts as a constant when deriving with respect to $x$ .

Integrating $f_{x}$ in this example gives:

\int\frac{\partial f}{\partial x}\ dx=\int(3x^{2}y+2x)\ dx=x^{3}y+x^{2}+C(y).

Likewise, integrating $f_{y}$ with respect to $y$ gives:

\int\frac{\partial f}{\partial y}\ dy=\int(x^{3}+1)\ dy=x^{3}y+y+C(x).

These two results should be equal with appropriate choices of $C(x)$ and $C(y)$ :

x^{3}y+x^{2}+C(y)=x^{3}y+y+C(x)\quad\Rightarrow\quad C(x)=x^{2}\quad\text{and}% \quad C(y)=y.

We find $f(x,y)=x^{3}y+x^{2}+y$ , a potential function of $\vec{F}$ . (If $\vec{F}$ were not conservative, no choice of $C(x)$ and $C(y)$ would give equality.)

By the Fundamental Theorem of Line Integrals, regardless of the path from $A$ to $B$ ,

	$\displaystyle\int_{A}^{B}\vec{F}\cdot d\vec{r}$	$\displaystyle=f(B)-f(A)$
		$\displaystyle=f(1,4)-f(0,1)$
		$\displaystyle=9-1=8.$

To illustrate the validity of the Fundamental Theorem, we pick a path from $A$ to $B$ . The line between these two points would be simple to construct; we choose a slightly more complicated path by choosing the parabola $y=x^{2}+2x+1$ . This leads to the parameterization $\vec{r}(t)=\left\langle t,t^{2}+2t+1\right\rangle$ , $0\leq t\leq 1$ , with $\vec{r}\hskip 1.25pt^{\prime}(t)=\left\langle t,2t+2\right\rangle$ . Thus

	$\displaystyle\int_{C}\vec{F}\cdot d\vec{r}$	$\displaystyle=\int_{C}\vec{F}\big{(}\vec{r}(t)\big{)}\cdot\vec{r}\hskip 1.25pt% ^{\prime}(t)\ dt$
		$\displaystyle=\int_{0}^{1}\left\langle 3(t)(t^{2}+2t+1)+2t,t^{3}+1\right% \rangle\cdot\left\langle t,2t+2\right\rangle\ dt$
		$\displaystyle=\int_{0}^{1}\big{(}5t^{4}+8t^{3}+3t^{2}+4t+2\big{)}\ dt$
		$\displaystyle=\big{(}t^{5}+2t^{4}+t^{3}+2t^{2}+2t\big{)}\Big{\|}_{0}^{1}$
		$\displaystyle=8,$

which matches our previous result.

The Fundamental Theorem of Line Integrals states that we can determine whether or not $\vec{F}$ is conservative by determining whether or not $\vec{F}$ has a potential function. This can be difficult. A simpler method exists if the domain of $\vec{F}$ is simply connected (not just connected as needed in the Fundamental Theorem of Line Integrals), which is a reasonable requirement. We state this simpler method as a theorem.

Theorem 15.3.3 Curl of Conservative Fields

Let $\vec{F}$ be a vector field whose components are continuous on a simply connected domain $D$ in the plane or in space. Then $\vec{F}$ is conservative if and only if $\operatorname{curl}\vec{F}=0$ or $\vec{0}$ , respectively.

In Example 15.3.5, we showed that $\vec{F}=\left\langle 3x^{2}y+2x,x^{3}+1\right\rangle$ is conservative by finding a potential function for $\vec{F}$ . Using the above theorem, we can show that $\vec{F}$ is conservative much more easily by computing its curl:

\operatorname{curl}\vec{F}=N_{x}-M_{y}=3x^{2}-3x^{2}=0.

Exercises 15.3

Terms and Concepts

1.

T/F: In practice, the evaluation of line integrals over vector fields involves computing the magnitude of a vector-valued function.
2.

Let $\vec{F}(x,y)$ be a vector field in the plane and let $\vec{r}(t)$ be a two-dimensional vector-valued function. Why is “ $\vec{F}\big{(}\vec{r}(t)\big{)}$ ” an “abuse of notation”?
3.

T/F: The orientation of a curve $C$ matters when computing a line integral over a vector field.
4.

T/F: The orientation of a curve $C$ matters when computing a line integral over a scalar field.
5.

Under “reasonable conditions,” if $\operatorname{curl}\vec{F}=\vec{0}$ , what can we conclude about the vector field $\vec{F}$ ?
6.

Let $\vec{F}$ be a conservative field and let $C$ be a closed curve. Why are we able to conclude that $\oint_{C}\vec{F}\cdot d\vec{r}=0$ ?

Problems

In Exercises 7–26, a vector field $\vec{F}$ and a curve $C$ are given. Evaluate $\displaystyle\int_{C}\vec{F}\cdot d\vec{r}$ .

7.

$\vec{F}=\left\langle y,y^{2}\right\rangle$ ; $C$ is the line segment from $(0,0)$ to $(3,1)$ .
8.

$\vec{F}=\left\langle x,x+y\right\rangle$ ; $C$ is the portion of the parabola $y=x^{2}$ from $(0,0)$ to $(1,1)$ .
9.

$\vec{F}=\left\langle y,x\right\rangle$ ; $C$ is the top half of the unit circle, beginning at $(1,0)$ and ending at $(-1,0)$ .
10.

$\vec{F}=\left\langle xy,x\right\rangle$ ; $C$ is the portion of the curve $y=x^{3}$ on $-1\leq x\leq 1$ .
11.

$\vec{F}=\left\langle z,x^{2},y\right\rangle$ ; $C$ is the line segment from $(1,2,3)$ to $(4,3,2)$ .
12.
$\vec{F}=\left\langle y+z,x+z,x+y\right\rangle$ ; $C$ is the helix $\vec{r}(t)=\left\langle\cos t,\sin t,t/(2\pi)\right\rangle$ on $0\leq t\leq 2\pi$ .
13.

$\vec{F}=\vec{\imath}-\vec{\jmath}$ ; $C$ is the line segment from the origin to $(3,2)$
14.

$\vec{F}=y\,\vec{\imath}-x\,\vec{\jmath}$ ; $C$ is the unit circle traced once counterclockwise.
15.

$\vec{F}=x\,\vec{\imath}+y\,\vec{\jmath}$ ; $C$ is the unit circle traced once counterclockwise.
16.

$\vec{F}=(x^{2}-y)\,\vec{\imath}+(x-y^{2})\,\vec{\jmath}$ ; $C$ is the unit circle traced once counterclockwise.
17.

$\vec{F}=xy^{2}\,\vec{\imath}+xy^{3}\,\vec{\jmath}$ ; $C$ is the polygonal path from $(0,0)$ to $(1,0)$ to $(0,1)$ to $(0,0)$
18.

$\vec{F}=(x^{2}+y^{2})\,\vec{\imath}$ ; $C$ is the unit circle centered at $(2,0)$ traced once counterclockwise.
19.

$\vec{F}=\left\langle x^{2},xy\right\rangle$ ; $C$ is the triangle with vertices $(1,0)$ , $(0,1)$ , $(-1,0)$ traversed counterclockwise.
20.

$\vec{F}=\left\langle y^{2},x^{2}\right\rangle$ ; $C$ is the curve $y=1/x$ for $1\leq x\leq 2$ , traversed (a) left to right; (b) right to left.
21.

$\vec{F}=\vec{\imath}-\vec{\jmath}+\vec{k}$ ; $C$ is the line segment connecting the origin to $(3,2,1)$
22.

$\vec{F}=y\,\vec{\imath}-x\,\vec{\jmath}+z\,\vec{k}$ ; $C$ is the helix $x=\cos t$ , $y=\sin t$ , $z=t$ for $0\leq t\leq 2\pi$
23.

$\vec{F}=x\,\vec{\imath}+y\,\vec{\jmath}+z\,\vec{k}$ ; $C$ is the unit circle parallel to the $x y$ plane centered at $(0,0,2)$ .
24.

$\vec{F}=(y-2z)\,\vec{\imath}+xy\,\vec{\jmath}+(2xz+y)\,\vec{k}$ ; $C$ is the curve $x=t$ , $y=2t$ , $z=t^{2}-1$ for $0\leq t\leq 1$
25.

$\vec{F}=yz\,\vec{\imath}+xz\,\vec{\jmath}+xy\,\vec{k}$ ; $C$ is the polygonal path from $(0,0,0)$ to $(1,0,0)$ to $(1,2,0)$
26.

$\vec{F}=xy\,\vec{\imath}+(z-x)\,\vec{\jmath}+2yz\,\vec{k}$ ; $C$ is the polygonal path from $(0,0,0)$ to $(1,0,0)$ to $(1,2,0)$ to $(1,2,-2)$

In Exercises 27–32, find the work performed by the force field $\vec{F}$ moving a particle along the path $C$ .

27.

$\vec{F}=\left\langle y,x^{2}\right\rangle$ N; $C$ is the segment of the line $y=x$ from $(0,0)$ to $(1,1)$ , where distances are measured in meters.
28.

$\vec{F}=\left\langle y,x^{2}\right\rangle$ N; $C$ is the portion of $y=\sqrt{x}$ from $(0,0)$ to $(1,1)$ , where distances are measured in meters.
29.

$\vec{F}=\left\langle 2xy,x^{2},1\right\rangle$ lbs; $C$ is the path from $(0,0,0)$ to $(2,4,8)$ via $\vec{r}(t)=\left\langle t,t^{2},t^{3}\right\rangle$ on $0\leq t\leq 2$ , where distance are measured in feet.
30.

$\vec{F}=\left\langle 2xy,x^{2},1\right\rangle$ lbs; $C$ is the path from $(0,0,0)$ to $(2,4,8)$ via $\vec{r}(t)=\left\langle t,2t,4t\right\rangle$ on $0\leq t\leq 2$ , where distance are measured in feet.
31.

$\vec{F}=\left\langle x,xy\right\rangle$ N; $C$ is the top half of the circle $x^{2}+y^{2}=1$ traversed from $(1,0)$ to $(-1,0)$ .
32.

$\vec{F}=\left\langle x,xy\right\rangle$ N; $C$ is the the parabola $y=1-x^{2}$ traversed from $(1,0)$ to $(-1,0)$ .

In Exercises 33–42, determine if the given vector field has a potential. If so, find one.

33.

$\vec{F}(x,y)=y\,\vec{\imath}-x\,\vec{\jmath}$
34.

$\vec{F}=x\,\vec{\imath}-y\,\vec{\jmath}$
35.

$\vec{F}=xy^{2}\,\vec{\imath}+x^{3}y\,\vec{\jmath}$
36.

$\vec{F}=(y^{2}+3x^{2})\,\vec{\imath}+2xy\,\vec{\jmath}$
37.

$\vec{F}=(x^{3}\cos(xy)+2x\sin(xy))\,\vec{\imath}+x^{2}y\cos(xy)\,\vec{\jmath}$
38.

$\vec{F}=(8xy+3)\,\vec{\imath}+4(x^{2}+y)\,\vec{\jmath}$
39.

$\vec{F}=y\,\vec{\imath}-x\,\vec{\jmath}+z\,\vec{k}$
40.

$\vec{F}=a\,\vec{\imath}+b\,\vec{\jmath}+c\,\vec{k}$ ( $a$ , $b$ , $c$ constant)
41.

$\vec{F}=(x+y)\,\vec{\imath}+x\,\vec{\jmath}+z^{2}\,\vec{k}$
42.

$\vec{F}=xy\,\vec{\imath}-(x-yz^{2})\,\vec{\jmath}+y^{2}z\,\vec{k}$

In Exercises 43–50, a conservative vector field $\vec{F}$ and a curve $C$ are given.

1.

Find a potential function $f$ for $\vec{F}$ .
2.

Compute $\operatorname{curl}\vec{F}$ .
3.

Evaluate $\displaystyle\int_{C}\vec{F}\cdot d\vec{r}$ directly, i.e., using Key Idea 15.3.1.
4.

Evaluate $\displaystyle\int_{C}\vec{F}\cdot d\vec{r}$ using the Fundamental Theorem of Line Integrals.

43.

$\vec{F}=\left\langle y+1,x\right\rangle$ , $C$ is the line segment from $(0,1)$ to $(1,0)$ .
44.

$\vec{F}=\left\langle 2x+y,2y+x\right\rangle$ , $C$ is curve parametrized by $\vec{r}(t)=\left\langle t^{2}-t,t^{3}-t\right\rangle$ on $0\leq t\leq 1$ .
45.

$\vec{F}=\left\langle 2xyz,x^{2}z,x^{2}y\right\rangle$ , $C$ is curve parametrized by $\vec{r}(t)=\left\langle 2t+1,3t-1,t\right\rangle$ on $0\leq t\leq 2$ .
46.

$\vec{F}=\left\langle 2x,2y,2z\right\rangle$ , $C$ is curve parametrized by $\vec{r}(t)=\left\langle\cos t,\sin t,\sin(2t)\right\rangle$ on $0\leq t\leq 2\pi$ .
47.

$\vec{F}=\left\langle x^{2}+y^{2},2xy\right\rangle$ , $C$ is the unit circle traced once counterclockwise.
48.

$\vec{F}=\left\langle x^{2}+y^{2},2xy\right\rangle$ , $C$ is the unit circle traced from $(1,0)$ to $(-1,0)$ .
49.

$\vec{F}=\left\langle xy^{2},x^{2}y\right\rangle$ , $C$ is $x=t\cos t$ , $y=t\sin t$ for $0\leq t\leq 5\pi/4$
50.

$\vec{F}=\left\langle 2xe^{y},2y+x^{2}e^{y}\right\rangle$ , $C$ is the polygonal path from $(1,0)$ to $(2,1)$ to $(0,0)$ .
51.

Prove part of Theorem 15.3.3: let $\vec{F}=\left\langle M,N,P\right\rangle$ be a conservative vector field. Show that $\operatorname{curl}\vec{F}=0$ .
52.

Show that if $\vec{f}\perp\vec{r}\hskip 0.75pt^{\prime}(t)$ at each point $\vec{r}(t)$ along a smooth curve $C$ , then $\int_{C}\vec{f}\cdot d\vec{r}=0$ .
53.

Show that if $\vec{f}$ points in the same direction as $\vec{r}\hskip 0.75pt^{\prime}(t)$ at each point $\vec{r}(t)$ along a smooth curve $C$ , then $\int_{C}\vec{f}\cdot d\vec{r}=\int_{C}\left\lVert\vec{f}\right\rVert\,ds$ .
54.
Let $C$ be a smooth curve with arc length $L$ , and suppose that $\vec{f}(x,y)=P(x,y)\,\vec{\imath}+Q(x,y)\,\vec{\jmath}$ is a vector field such that $\left\lVert\vec{f}(x,y)\right\rVert\leq M$ for all $(x,y)$ on $C$ . Show that $\left\lvert\int_{C}\vec{f}\cdot d\vec{r}\right\rvert\leq ML$ . (Hint: Recall that $\left\lvert\int_{a}^{b}g(x)\,dx\right\rvert\leq\int_{a}^{b}\left\lvert g(x)% \right\rvert\,dx$ for Riemann integrals.)
55.
Prove Theorem 15.3.1 part 1. Let $\vec{F}$ and $\vec{G}$ be vector fields, let $k_{1}$ and $k_{2}$ be constants, and let $C$ . Show that $\int_{C}(k_{1}\,\vec{F}\pm k_{2}\,\vec{G})\cdot d\vec{r}=k_{1}\int_{C}\vec{F}% \cdot d\vec{r}\pm k_{2}\int_{C}\vec{G}\cdot d\vec{r}.$
56.
Let $f(x,y)$ and $g(x,y)$ be continuously differentiable real-valued functions in a region $R$ . Show that $\oint_{C}(f\,\nabla g)\cdot d\vec{r}=-\oint_{C}(g\,\nabla f)\cdot d\vec{r}$ for any closed curve $C$ in $R$ .
57.
Let $\vec{F}(x,y)=\frac{-y}{x^{2}+y^{2}}\,\vec{\imath}+\frac{x}{x^{2}+y^{2}}\,\vec{\jmath}$ for all $(x,y)\neq(0,0)$ , and $C :$ $x=\cos t$ , $y=\sin t$ , $0\leq t\leq 2\pi$ . (a) Show that $\vec{F}=\nabla f$ , for $f(x,y)=\tan^{-1}(y/x)$ . (b) Show that $\displaystyle\oint_{C}\vec{F}\cdot d\vec{r}=2\pi$ . Does this contradict Theorem 15.3.2? Explain.
58.

Let $g(x)$ and $h(y)$ be differentiable functions, and let $\vec{F}(x,y)=h(y)\,\vec{\imath}+g(x)\,\vec{\jmath}$ . Is it possible for $\vec{F}$ to have a potential $f(x,y)$ ? If so, find an example. You may assume that $f$ would be smooth. (Hint: Consider the mixed partial derivatives of $f$ .)
59.

For $\vec{F}=\left\langle xy,y\right\rangle$ , evaluate $\displaystyle\oint_{C}\vec{F}\cdot d\vec{r}$ where $C$ is $x=\cos t$ , $y=\sin t$ for $0\leq t\leq 2\pi$ . Is $\vec{F}$ conservative?
60.
For $\vec{F}=\left\langle y^{2},x^{2}\right\rangle$ , evaluate $\displaystyle\int_{C}\vec{F}\cdot d\vec{r}$ for: (a) $C$ given by $x=t$ , $y=t^{2}$ for $0\leq t\leq 1$ . (b) $C$ given by $x=t^{2}$ , $y=t$ for $0\leq t\leq 1$ . (c) Is $\vec{F}$ conservative?